Phương pháp giải:

- Diện tích của mặt cầu có bán kính bằng \(R\) là \(S = 4\pi {R^2}\).

- Áp dụng định lí Pytago tính bán kính \(r\) của đường tròn.

Lời giải chi tiết:

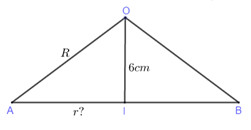
Gọi \(I\) là tâm thiết diện khi cắt mặt cầu \(\left( S \right)\) bởi mặt phẳng \(\left( P \right)\), \(AB\) là đường kính của đường tròn.

Gọi \(R\) là bán kính của mặt cầu \(\left( S \right)\). Diện tích của mặt cầu bằng \(400\pi \left( {c{m^2}} \right)\) nên :

                                          \(S = 400\pi  \Leftrightarrow 4\pi {R^2} = 400\pi  \Rightarrow R = 10\left( {cm} \right)\)

\(A,B\) nằm trên đường tròn nên \(A,B\) cũng nằm trên mặt cầu hay \(OA = OB = R = 10\,\,\,\left( {cm} \right)\)

Khoảng cách từ tâm \(O\) đến mặt phẳng \(\left( P \right)\) là  \(OI = 6\left( {cm} \right)\).

Áp dụng định lí Pytago  trong tam giác \(OIA\) vuông tại \(I\) ta có:

\(O{I^2} + I{A^2} = O{A^2} \Leftrightarrow {6^2} + I{A^2} = {10^2} \Leftrightarrow IA = 8\,\,\,\left( {cm} \right)\).

Vậy bán kính \(r\) của đường tròn là  \(r = IA = 8\left( {cm} \right)\).

Chọn D.