Câu hỏi
Hàm số \(y = a{x^4} + b{x^2} + c,\left( {a \ne 0} \right)\) có hai điểm cực đại và một điểm cực tiểu khi
- A \(a > 0,b > 0\)
- B \(a > 0,b < 0\)
- C \(a < 0,b > 0\)
- D \(a < 0,b < 0\)
Phương pháp giải:
Tham khảo hình vẽ đồ thị bậc 4 trùng phương có hai điểm cực đại và một điểm cực tiểu để giải bài toán
Lời giải chi tiết:
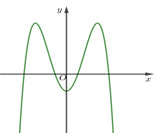
Đồ thị hàm số bậc 4 trùng phương có hai điểm cực đại và một điểm cực tiểu có dạng như sau:
Từ đồ thị ta thấy\(\mathop {\lim }\limits_{x \to + \infty } = - \infty \Rightarrow a < 0\).
Ta có : \(y' = 4a{x^2} + 2bx = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = - \dfrac{b}{{2a}}\end{array} \right.\).
Như vậy, để hàm số đã cho có 3 điểm cực trị thì \( - \dfrac{b}{{2a}} > 0 \Rightarrow \left\{ \begin{array}{l}a < 0\\b > 0\end{array} \right.\)
Vậy \(a < 0;\,\,b > 0\).
Chọn C.
Câu hỏi trước
