Câu hỏi
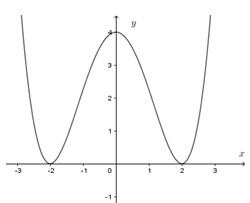
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị như hình vẽ sau. Số nghiệm nguyên của phương trình \({\left( {\left[ {f{{\left( {{x^2} - 2} \right)}^2}} \right]} \right)^t} = 0\) là
- A \(3\)
- B \(4\)
- C \(2\)
- D \(5\)
Phương pháp giải:
Đọc đồ thị hàm số
Sử dụng công thức tính đạo hàm hàm hợp \({\left( {f\left( u \right)} \right)^\prime } = u'.f'\left( u \right)\)
Lời giải chi tiết:
Từ đồ thị hàm số ta suy ra:
\(f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 2\end{array} \right.\) và \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 2\\x = 0\end{array} \right.\)
Ta có:
\(\begin{array}{l}{\left( {{{\left[ {f\left( {{x^2} - 2} \right)} \right]}^2}} \right)^\prime } = 2f\left( {{x^2} - 2} \right).{\left[ {f\left( {{x^2} - 2} \right)} \right]^\prime }\\ = 2f\left( {{x^2} - 2} \right)2x.f'\left( {{x^2} - 2} \right)\\ = 4xf'\left( {{x^2} - 2} \right)f\left( {{x^2} - 2} \right)\end{array}\)
Khi đó:
\(\begin{array}{l}{\left( {{{\left[ {f\left( {{x^2} - 2} \right)} \right]}^2}} \right)^\prime } = 0 \Leftrightarrow 4xf'\left( {{x^2} - 2} \right)f\left( {{x^2} - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {{x^2} - 2} \right) = 0\\f\left( {{x^2} - 2} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 2 = - 2\\{x^2} - 2 = 2\\{x^2} - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\\x = - 2\\x = \sqrt 2 \\x = - \sqrt 2 \end{array} \right.\end{array}\)
Mà \(x \in \mathbb{Z} \Rightarrow x \in \left\{ {0;2; - 2} \right\}\)
Chọn A.







