Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và hàm số \(y = f'\left( x \right)\) có đồ thị như sau:
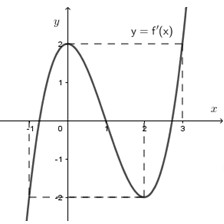
Dặt \(g\left( x \right) = f\left( {x - \dfrac{m}{3}} \right) - \dfrac{1}{2}{\left( {x - \dfrac{m}{3} - 1} \right)^2} + m + 1\) với \(m\) là tham số. Gọi \(S\) là tập hợp tất cả các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {7;8} \right)\). Tổng của tất cả các phần tử có trong tập hợp \(S\) bằng
- A \(186\)
- B \(816\)
- C \(168\)
- D \(618\)
Phương pháp giải:
- Tính \(g'\left( x \right)\) .
- Hàm số đã cho đồng biến trên \(\left( {7;8} \right)\) \( \Leftrightarrow g'\left( x \right) \ge 0,\forall x \in \left( {7;8} \right)\).
Lời giải chi tiết:
Ta có: \(g'\left( x \right) = f'\left( {x - \dfrac{m}{3}} \right) - \left( {x - \dfrac{m}{3} - 1} \right)\)
Đặt \(t = x - \dfrac{m}{3}\). Với \(x \in \left( {7;8} \right)\) thì \(t \in \left( {7 - \dfrac{m}{3};8 - \dfrac{m}{3}} \right)\)
Hàm số đã cho đồng biến trên \(\left( {7;8} \right)\) \( \Leftrightarrow \) \(g'\left( x \right) \ge 0,\forall x \in \left( {7;8} \right)\)
\( \Leftrightarrow f'\left( {x - \dfrac{m}{3}} \right) \ge x - \dfrac{m}{3} - 1\) , \(\forall x \in \left( {7;8} \right)\)
\( \Leftrightarrow f'\left( t \right) \ge t - 1,\forall t \in \left( {7 - \dfrac{m}{3};8 - \dfrac{m}{3}} \right)\)
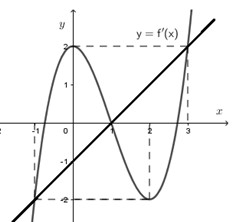
Vẽ đường thẳng \(y = x - 1\) trên cùng hệ tọa độ với đồ thị hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( t \right) \ge t - 1 \Leftrightarrow \left[ \begin{array}{l} - 1 \le t \le 1\\t \ge 3\end{array} \right.\)
Vậy \(f'\left( t \right) \ge t - 1,\forall t \in \left( {7 - \dfrac{m}{3};8 - \dfrac{m}{3}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l} - 1 \le 7 - \dfrac{m}{3} < 8 - \dfrac{m}{3} \le 1\\3 \le 7 - \dfrac{m}{3} < 8 - \dfrac{m}{3}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}21 \le m \le 24\\m \le 12\end{array} \right.\)
Mà \(m\) nguyên dương nên \(m \in \left\{ {1;2;...;12;21;22;23;24} \right\}\).
Vậy tổng là \(1 + 2 + 3 + ... + 12 + 21 + 22 + 23 + 24 = 168\).
Chọn C.







