Phương pháp giải:

Thể tích khối nón có bán kính đáy \(r\) và chiều cao \(h\) là \(V = \dfrac{1}{3}\pi {r^2}h\)

Lời giải chi tiết:

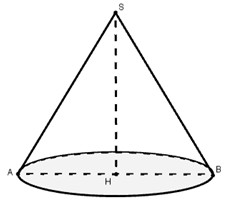
Tam giác \(SAB\) là tam giác đều có diện tích

\(S = \dfrac{{A{B^2}\sqrt 3 }}{4} = 25\sqrt 3 {a^2} \Leftrightarrow A{B^2} = 100{a^2} \Rightarrow AB = 10a = SA\)

Suy ra \(SH = \sqrt {S{A^2} - A{O^2}}  = \sqrt {{{10}^2} - {5^2}}  = 5\sqrt 3 a\)

Thể tích khối nón là: \(V = \dfrac{1}{3}\pi SH.O{A^2} = \dfrac{1}{3}\pi .{\left( {5a} \right)^2}.\left( {5\sqrt 3 a} \right) = \dfrac{{125{a^3}}}{3}\pi \)

Chọn A.