Phương pháp giải:

- Đặt \(IH = x\) lập công thức tính thể tích khối nón theo \(x\) .

- Sử dụng phương pháp hàm số đánh giá GTLN của thể tích.

Lời giải chi tiết:

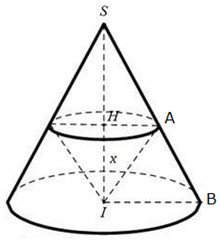
Tam giác \(SIB\) vuông tại \(I\) ta có \(SI = \sqrt {S{B^2} - I{B^2}}  = \sqrt {9{a^2} - 5{a^2}}  = 2a\).

Đặt \(IH = x\left( {0 < x < a\sqrt 5 } \right)\) \( \Rightarrow SH = SI - IH = a\sqrt 5  - x\)

Tam giác \(SHA\) đồng dạng \(SIB\) nên

\(\dfrac{{HA}}{{IB}} = \dfrac{{SH}}{{SI}} \Leftrightarrow \dfrac{{HA}}{{2a}} = \dfrac{{a\sqrt 5  - x}}{{a\sqrt 5 }}\) \( \Leftrightarrow HA = \dfrac{{2a\sqrt 5  - 2x}}{{\sqrt 5 }}\)

Thể tích khối nón đỉnh \(I\) đường tròn đáy tâm \(H\) là:

\(V = \dfrac{1}{3}\pi H{A^2}.IH\) \( = \dfrac{1}{3}\pi .{\left( {\dfrac{{2a\sqrt 5  - 2x}}{{\sqrt 5 }}} \right)^2}.x = \dfrac{{4\pi }}{{15}}{\left( {a\sqrt 5  - x} \right)^2}.x\)

Xét hàm \(f\left( x \right) = {\left( {a\sqrt 5  - x} \right)^2}.x\) trên \(\left( {0;a\sqrt 5 } \right)\) có:

\(\begin{array}{l}f'\left( x \right) =  - 2\left( {a\sqrt 5  - x} \right).x + {\left( {a\sqrt 5  - x} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, =  - 2ax\sqrt 5  + 2{x^2} + 5{a^2} - 2ax\sqrt 5  + {x^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^2} - 4ax\sqrt 5  + 5{a^2}\end{array}\) 

\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = a\sqrt 5 \left( {loai} \right)\\x = \dfrac{{a\sqrt 5 }}{3}\left( {TM} \right)\end{array} \right.\)

Bảng biến thiên:

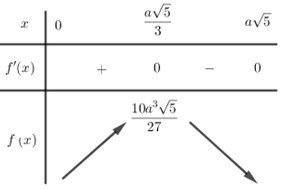
Từ bảng biến thiên ta thấy hàm số \(f\left( x \right)\) đạt GTLN tại \(x = \dfrac{{a\sqrt 5 }}{3}\) và \(f\left( {\dfrac{{a\sqrt 5 }}{3}} \right) = \dfrac{{10{a^3}\sqrt 5 }}{{27}}\)

Vậy thể tích lớn nhất \({V_{\max }} = \dfrac{{4\pi }}{{15}}.\dfrac{{10{a^3}\sqrt 5 }}{{27}} = \dfrac{{8\pi {a^3}\sqrt 5 }}{{81}}\).

Chọn C