Câu hỏi
Tìm số dương \(b\) để giá trị lớn nhất của hàm số \(y = {x^3} - 3b{x^2} + b - 1\) trên đoạn \(\left[ { - 1;b} \right]\) bằng 10?
- A \(b = 11\)
- B \(b = 10\)
- C \(b = \frac{3}{2}\)
- D \(b = \frac{5}{2}\)
Phương pháp giải:
Lập BBT của hàm số, chú ý điều kiện \(b > 0\).
Lời giải chi tiết:
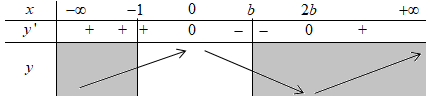
Ta có: \(y' = 3{x^2} - 6bx = 0 \Leftrightarrow 3x\left( {x - 2b} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2b > 0\,\,\left( {Do\,\,b > 0} \right)\end{array} \right.\).
Do \(b > 0 \Rightarrow 2b > b\,\,\forall b > 0 \Rightarrow 2b \notin \left[ { - 1;b} \right]\).
Ta có BBT:
Từ BBT ta thấy \(\mathop {\max }\limits_{\left[ { - 1;b} \right]} = f\left( 0 \right) = b - 1\).
\( \Rightarrow b - 1 = 10 \Leftrightarrow b = 11\).
Chọn A.
Câu hỏi trước
