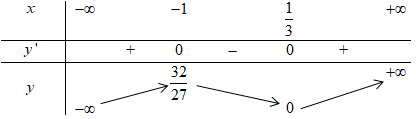Phương pháp giải:

Đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) tiếp xúc nhau khi và chỉ khi hệ phương trình \(\left\{ \begin{array}{l}f\left( x \right) = g\left( x \right)\\f'\left( x \right) = g'\left( x \right)\end{array} \right.\) có nghiệm.

Lời giải chi tiết:

Đồ thị hàm số \(y = {x^3} - 3m{x^2} + 3mx + {m^2} - 2{m^3}\) tiếp xúc với trục hoành khi và chỉ khi hệ phương trình \(\left\{ \begin{array}{l}f\left( x \right) = 0\\f'\left( x \right) = 0\end{array} \right.\) có nghiệm.

\( \Rightarrow \left\{ \begin{array}{l}{x^3} - 3m{x^2} + 3mx + {m^2} - 2{m^3} = 0\\3{x^2} - 6mx + 3m = 0\end{array} \right.\) có nghiệm.

\( \Leftrightarrow \left\{ \begin{array}{l}x\left( {{x^2} - 2mx + m} \right) - m{x^2} + 2mx + {m^2} - 2{m^3} = 0\,\,\,\left( 1 \right)\\{x^2} - 2mx + m = 0\,\,\,\left( 2 \right)\end{array} \right.\) có nghiệm.

\( \Leftrightarrow \left\{ \begin{array}{l} - m{x^2} + 2mx + {m^2} - 2{m^3} = 0\\{x^2} - 2mx + m = 0\end{array} \right.\) có nghiệm.

\( \Leftrightarrow \left\{ \begin{array}{l} - m\left( {2mx - m} \right) + 2mx + {m^2} - 2{m^3} = 0\\{x^2} = 2mx - m\end{array} \right.\)  có nghiệm.

\( \Leftrightarrow \left\{ \begin{array}{l} - 2{m^2}x + 2{m^2} + 2mx - 2{m^3} = 0\\{x^2} = 2mx - m\end{array} \right.\)  có nghiệm.

\( \Leftrightarrow \left\{ \begin{array}{l} - 2mx\left( {m - 1} \right) + 2m\left( {1 - m} \right) = 0\\{x^2} = 2mx - m\end{array} \right.\)  có nghiệm.

\( \Leftrightarrow \left\{ \begin{array}{l}2m\left( {m - 1} \right)\left( { - x - m} \right) = 0\\{x^2} = 2mx - m\end{array} \right.\)  có nghiệm.

\( \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 1\\x =  - m\end{array} \right.\mathop  \Rightarrow \limits^{\left( 2 \right)} \left[ \begin{array}{l}x = 0\\x = 1\\m = 0\,\,hoac\,\,m =  - \frac{1}{3}\end{array} \right.\)

Với \(m = 0 \Rightarrow y = {x^3}\) (điểm uốn thuộc \(Ox\)) \( \Rightarrow \) Thỏa mãn.

Với \(m = 1 \Rightarrow y = {\left( {x - 1} \right)^3}\) (điểm uốn thuộc \(Ox\)) \( \Rightarrow \) Thỏa mãn.

Với \(m =  - \frac{1}{3} \Rightarrow y = {x^3} + {x^2} - x + \frac{5}{{27}}\).

Ta có BBT:

\( \Rightarrow \)Đồ thị hàm số tiếp xúc với trục hoành tại \(x = \frac{1}{3}\).

Vậy \({m_1} + {m_2} + {m_3} = 0 + 1 + \left( { - \frac{1}{3}} \right) = \frac{2}{3}\).

Chọn D.