Phương pháp giải:

- Hàm đa thức \(y = f\left( x \right)\)  đạt cực trị tại \(x = a\) khi và chỉ khi \(a\) là một nghiệm của phương trình \(y' = 0\).

- Tìm \(y'\) . Thay \(x = a\) vào phương trình \(y' = 0\) để tìm tham số \(m\).

- Xác định \(x = a\) là cực đại hay cực tiểu và giá trị cực trị tương ứng.

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\)

Ta có: \(y' = 6{x^2} - 4\left( {2 - m} \right)x + \left( {m - 5} \right)\).

Để hàm số đạt cực trị tại \(x = 0\) thì \(x = 0\) là một nghiệm của phương trình \(y' = 0.\)

\( \Rightarrow {6.0^2} - 4.\left( {2 - m} \right).0 + m - 5 = 0 \Leftrightarrow m = 5.\)

Thay \(m = 5\) vào ta được: \(y = 2{x^3} + 6{x^2} - 4\).

\( \Rightarrow y' = 6{x^2} + 12x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 2\end{array} \right.\)

BBT:

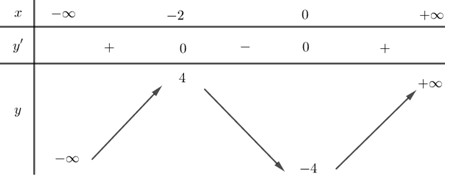
Từ BBT ta thấy khi \(x = 0\) thì hàm số đã cho đạt cực tiểu và giá trị cực tiểu đó bằng \( - 4\).