Phương pháp giải:

Thể tích khối nón được tính bởi công thức \(V = \dfrac{1}{3}\pi {r^2}h\) (trong đó \(r\) là bán kính đáy, \(h\) là chiều cao).

Lời giải chi tiết:

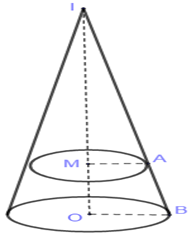
Giả sử có một đường sinh của hình nón cắt \(\left( P \right)\) tại \(A\) và cắt đáy tâm \(O\) tại \(B\).

Mặt phẳng \(\left( P \right)\) chia hình nón thành 2 phần trong đó có 1 phần là hình nón có đỉnh là \(I\), đáy là đường tròn tâm \(M\).

Đặt \(h = IO;\)\(r = OB;\)\({h_1} = IM;\)\({r_1} = MA\)

Do \(MA\parallel OB\) (cùng vuông góc với \(OI\)) nên áp dụng định lí Ta-lét: \(\dfrac{{IM}}{{IO}} = \dfrac{{MA}}{{OB}} \Leftrightarrow \dfrac{{{h_1}}}{h} = \dfrac{{{r_1}}}{r}\).

Thể tích khối nón ban đầu là: \(V = \dfrac{1}{3}\pi .O{B^2}.OI = \dfrac{1}{3}\pi {r^2}h\).

Thể tích khối nón có đỉnh \(I,\) đường tròn đáy có tâm \(M\) là: \({V_1} = \dfrac{1}{3}\pi M{A^2}.IM = \dfrac{1}{3}\pi {r_1}^2.{h_1}\)

Ta có: \(\dfrac{{{V_1}}}{V} = \dfrac{1}{2} \Leftrightarrow \dfrac{{\dfrac{1}{3}\pi {r_1}^2{h_1}}}{{\dfrac{1}{3}\pi {r^2}h}} = \dfrac{1}{2} \Leftrightarrow \dfrac{{{r_1}^2{h_1}}}{{{r^2}h}} = \dfrac{1}{2} \Leftrightarrow {\left( {\dfrac{{{h_1}}}{h}} \right)^3} = \dfrac{1}{2} \Leftrightarrow \dfrac{{{h_1}}}{h} = \dfrac{1}{{\sqrt[3]{2}}}\).

Vậy \(\dfrac{{IM}}{{IO}} = \dfrac{{{h_1}}}{h} = \dfrac{1}{{\sqrt[3]{2}}}\).

Chọn B.