Phương pháp giải:

- Tìm tâm mặt cầu ngoại tiếp tứ diện \(ABCD\).

- Khi đó bán kính của mặt cầu ngoại tiếp của tứ diện \(ABCD\) là \(R = IA = IB = IC = ID\).

Lời giải chi tiết:

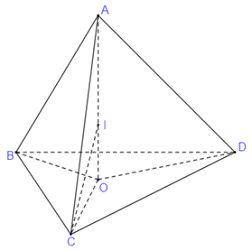
Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(BCD\), có bán kính là \(r\).

Do \(AB = AC = AD = 5\) nên chân đường cao hạ từ \(A\) xuống mặt phẳng \(\left( {BCD} \right)\) trùng với tâm đường tròn ngoại tiếp tam giác \(BCD\)

Suy ra \(AO \bot \left( {BCD} \right).\)

Gọi \(I\) là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\) thì \(I\) nằm trên \(AO\).

Tam giác \(BCD\) có \(BC = 2;\)\(BD = 3;\)\(CD = 4\) nên \(p = \dfrac{{BC + BD + CD}}{2} = \dfrac{9}{2}\).

Khi đó diện tích tam giác \(BCD\)được tính bởi công thức:   

\({S_{BCD}} = \sqrt {p\left( {p - BC} \right)\left( {p - BD} \right)\left( {p - CD} \right)}  = \dfrac{{3\sqrt {15} }}{4}\)

Mặt khác, diện tích tam giác \(BCD\) còn tính bởi \({S_{BCD}} = \dfrac{{BC.BD.CD}}{{4r}} \Rightarrow r = \dfrac{{8\sqrt {15} }}{{15}}\) (\(r\) là bán kính đường tròn ngoại tiếp). Suy ra \(OB = OC = OD = \dfrac{{8\sqrt {15} }}{{15}}\).

Đặt \(IA = IB = IC = ID = R\), ta có: \(AO \bot \left( {BCD} \right)\) nên  

\(\begin{array}{l}AO = \sqrt {A{C^2} - O{C^2}}  = \sqrt {\dfrac{{311}}{{15}}} \\O{I^2} + O{C^2} = I{C^2}\\ \Leftrightarrow {\left( {OA - IA} \right)^2} + O{C^2} = I{C^2}\\ \Leftrightarrow {\left( {\sqrt {\dfrac{{311}}{{15}}}  - R} \right)^2} + {\left( {\dfrac{{8\sqrt {15} }}{{15}}} \right)^2} = {R^2}\\ \Rightarrow R = \dfrac{{25\sqrt {15} }}{{2\sqrt {311} }}\end{array}\)

Vậy bán kính  mặt cầu ngoại tiếp tứ diện \(ABCD\) bằng \(\dfrac{{25\sqrt {15} }}{{2\sqrt {311} }}\).

Chọn A.