Phương pháp giải:

- Tìm tâm \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(OABC\).

- Chứng minh \(OI\) không đổi.

Lời giải chi tiết:

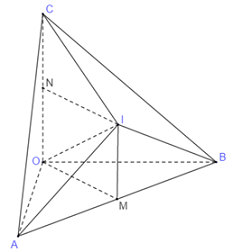
\(A\left( {\sin \alpha \sin \beta ;0;0} \right)\) nên \(A\)  nằm trên trục \(Ox\)

\(B\left( {0;\sin \alpha \cos \beta ;0} \right)\) nên \(B\) nằm trên trục \(Oy\)

\(C\left( {0;0;cos\alpha } \right)\) nên C nằm trên trục \(Oz\)

Do đó \(OA,OB,OC\) đôi một vuông góc với nhau

Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(OC\)

Tam giác \(OAB\) vuông tại \(O\) nên trung điểm \(M\) của \(AB\) là tâm đường tròn ngoại tiếp tam giác \(OAB\).

Dựng đường thẳng \(d\) đi qua \(M\) và vuông góc với mp\(\left( {OAB} \right)\)

Dựng mặt phẳng trung trực đi qua \(N\) của \(OC\) cắt \(d\) tại \(I\). Khi đó \(I\) là tâm mặt cầu ngoại tiếp tứ diện \(OABC\).

Tứ giác \(OMIN\) có 3 góc vuông nên là hình chữ nhật, do đó \(IM = ON = \dfrac{{OC}}{2}\).

Ta có:

\(\begin{array}{l}O{I^2} = O{M^2} + I{M^2}\\ \Leftrightarrow O{I^2} = {\left( {\dfrac{{AB}}{2}} \right)^2} + {\left( {\dfrac{{OC}}{2}} \right)^2}\\ \Leftrightarrow O{I^2} = \dfrac{{O{A^2} + O{B^2}}}{4} + \dfrac{{O{C^2}}}{4}\\ \Leftrightarrow O{I^2} = \dfrac{{{{\left( {\sin \alpha \sin \beta } \right)}^2} + {{\left( {\sin \alpha \cos \beta } \right)}^2} + {{\left( {\cos \alpha } \right)}^2}}}{4}\\ \Leftrightarrow O{I^2} = \dfrac{{{{\sin }^2}\alpha \left( {{{\sin }^2}\beta  + {{\cos }^2}\beta } \right) + {{\cos }^2}\alpha }}{4}\\ \Leftrightarrow O{I^2} = \dfrac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{4} = \dfrac{1}{4}\\ \Rightarrow OI = \dfrac{1}{2}\end{array}\) 

Suy ra \(I\) nằm trên mặt cầu tâm \(O\) bán kính không đổi \(R = \dfrac{1}{2}\).

Chọn D.