Phương pháp giải:

- Tìm góc tạo bởi mặt bên và đáy.

- Tính chiều cao của khối chóp

- Thể tích của khối chóp được tính bởi công thức: \({V_{S.ABC}} = \dfrac{1}{3}h.{S_{ABC}}\).

Lời giải chi tiết:

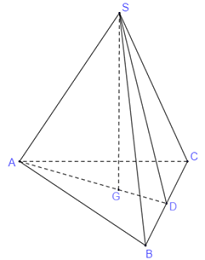
Gọi \(G\) là trọng tâm tam giác \(ABC\), \(D\) là trung điểm \(BC\).

\(S.ABC\) là hình chóp đều nên chân đường cao hạ từ \(S\) xuống mp đáy là trọng tâm \(G\) của đáy

Suy ra \(SG \bot \left( {ABC} \right) \Rightarrow SG \bot BC\)

Tam giác \(ABC\) là tam giác đều nên \(AD \bot BC\)

\( \Rightarrow BC \bot \left( {SAD} \right) \Rightarrow BC \bot SD\)

Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\SD \in \left( {SBC} \right),SD \bot BC\\AD \in \left( {ABC} \right),AD \bot BC\end{array} \right. \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle SDA\).

Góc giữa mặt bên và mặt đáy bằng \(60^\circ \) nên \(\angle SDA = {60^0}\).

Lại có:\(AD = \dfrac{{\sqrt 3 }}{2}BC = \sqrt 3 a \Rightarrow DG = \dfrac{1}{3}AD = \dfrac{{\sqrt 3 }}{3}a\).

\(\begin{array}{l}SG = GD\tan \widehat {SDA} = \dfrac{{\sqrt 3 }}{3}a.\tan 60^\circ  = a\\{S_{ABC}} = \dfrac{{\sqrt 3 }}{4}.A{B^2} = \dfrac{{\sqrt 3 }}{4}.4{a^2} = \sqrt 3 {a^2}\\ \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SG.{S_{ABC}} = \dfrac{1}{3}.a.\sqrt 3 {a^3} = \dfrac{{\sqrt 3 }}{3}{a^3}\end{array}\)

Chọn A.