Phương pháp giải:

- Tính thể tích \({V_{AMNB}}\) qua thể tích của \(ABC.A'B'C'\)

- Khoảng cách từ \(A\) đến mp\(\left( {MNB} \right)\) tính bởi công thức: \(d\left( {A;\left( {MNB} \right)} \right) = \dfrac{{3{V_{A.MNB}}}}{{{S_{MNB}}}}\)

Lời giải chi tiết:

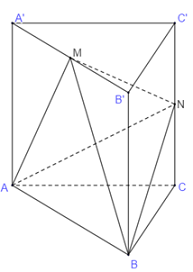
\(\Delta BMN\) là tam giác đều có cạnh bằng\(2a \Rightarrow {S_{\Delta BMN}} = \dfrac{{\sqrt 3 }}{4}.{\left( {2a} \right)^2} = \sqrt 3 {a^2}\) .

     \({V_{C.A'B'C'}} = \dfrac{1}{3}{V_{ABC.A'B'C'}} \Rightarrow {V_{C.ABB'A'}} = \dfrac{2}{3}{V_{ABC.A'B'C'}}\)

     \(\begin{array}{l}{V_{N.AMB}} = \dfrac{1}{3}{d_{\left( {N,\left( {AMB} \right)} \right)}}.{S_{\Delta MAB}} = \dfrac{1}{3}{d_{\left( {C,\left( {AMB} \right)} \right)}}.\dfrac{1}{2}{S_{AA'B'B}}\\\end{array}\)

               \( = \dfrac{1}{2}{V_{C.AA'B'B}} = \dfrac{1}{2}.\dfrac{2}{3}{V_{ABC.A'B'C'}} = \dfrac{1}{3}.{a^3} = \dfrac{{{a^3}}}{3}\)

Mặt khác, thể tích của \(ANMB\) còn được tính bởi công thức:\({V_{A.MNB}} = \dfrac{1}{3}{d_{\left( {A,\left( {MBN} \right)} \right)}}.{S_{\Delta MNB}} \Leftrightarrow \dfrac{{{a^3}}}{3} = \dfrac{1}{3}.{d_{\left( {A,\left( {MBN} \right)} \right)}}.\sqrt 3 {a^2} \Rightarrow d\left( {A,\left( {MBN} \right)} \right) = \dfrac{{a\sqrt 3 }}{3}\)

Vậy \(d\left( {A;\left( {BMN} \right)} \right) = \dfrac{{a\sqrt 3 }}{3}\).

Chọn C.