Câu hỏi
Cho khối chóp \(S.ABC\) có thể tích \(V\), biết \(M,N,P\) lần lượt thuộc các cạnh \(SA,SB,SC\)sao cho \(SM = MA,SN = 2NB,SC = 3SP\). Gọi \(V'\)là thể tích của khối chóp \(S.MNP\). Mệnh đề nào sau đây đúng?
- A \(V' = \dfrac{V}{6}\)
- B \(V' = \dfrac{V}{{12}}\)
- C \(V' = \dfrac{V}{9}\)
- D \(V' = \dfrac{V}{3}\)
Phương pháp giải:
Sử dụng công thức về tỉ số thể tích: \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{SM.SN.SP}}{{SA.SB.SC}}\) (với \(M,\,\,N,\,\,P\) lần lượt nằm trên các cạnh \(SA,\,\,SB,\,\,SC\) của khối chóp \(S.ABC\)).
Lời giải chi tiết:
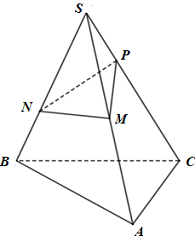
Ta có :
\(\begin{array}{l}SM = MA \Rightarrow \dfrac{{SM}}{{SA}} = \dfrac{1}{2}\\SN = 2NB \Rightarrow \dfrac{{SN}}{{SB}} = \dfrac{2}{3}\\SC = 3SP \Rightarrow \dfrac{{SP}}{{SC}} = \dfrac{1}{3}\\ \Rightarrow \dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}} = \dfrac{1}{2}.\dfrac{2}{3}.\dfrac{1}{3} = \dfrac{1}{9}\\ \Rightarrow {V_{S.MNP}} = \dfrac{1}{9}{V_{S.ABC}} = \dfrac{V}{9}.\end{array}\)
Chọn C.
Câu hỏi trước
