Phương pháp giải:

Hàm số \(y = \sqrt {f\left( x \right)} \) xác định trên \(\left( {0; + \infty } \right)\) khi và chỉ khi \(f\left( x \right) \ge 0\,\,\forall x \in \left( {a;b} \right)\).

Lời giải chi tiết:

Hàm số \(y = \sqrt {{x^4} - mx + 48} \) xác định trên \(\left( {0; + \infty } \right)\) khi và chỉ khi:

\(\begin{array}{l}{x^4} - mx + 48 \ge 0\,\,\forall x \in \left( {0; + \infty } \right)\\ \Leftrightarrow {x^4} + 48 \ge mx\,\,\forall x \in \left( {0; + \infty } \right)\\ \Leftrightarrow m \le \dfrac{{{x^4} + 48}}{x} = f\left( x \right)\,\,\,\forall x \in \left( {0; + \infty } \right)\,\,\left( {Do\,\,x > 0} \right)\\ \Leftrightarrow m \le \mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( x \right).\end{array}\)

Xét hàm số \(y = f\left( x \right) = {x^3} + \dfrac{{48}}{x}\) trên khoảng \(\left( {0; + \infty } \right)\) ta có:

\(f'\left( x \right) = 3{x^2} - \dfrac{{48}}{{{x^2}}} = 0 \Leftrightarrow 3{x^2} = \dfrac{{48}}{{{x^2}}} \Rightarrow x =  \pm 2.\)

BBT của hàm số \(f\left( x \right)\) trên khoảng \(\left( {0; + \infty } \right)\)

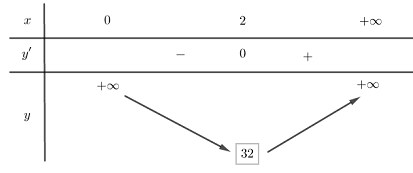
Từ BBT ta thấy \(m \le \mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( x \right) = f\left( 2 \right) = 32\).

Mà \(m\) là số tự nhiên nên có 33 giá trị của \(m\) thỏa mãn.

Chọn D.