Câu hỏi
Điểm cực tiểu \({x_{CT}}\) của hàm số \(y = {x^3} + 4{x^2} - 3x + 7\) là:
- A \({x_{CT}} = - \dfrac{1}{3}\)
- B \({x_{CT}} = 1\)
- C \({x_{CT}} = - 3\)
- D \({x_{CT}} = \dfrac{1}{3}\)
Phương pháp giải:
- Giải phương trình \(y' = 0\) để tìm cực trị của hàm số.
- Lập BBT để tìm cực đại, cực tiểu của hàm số đã cho.
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\)
Ta có: \(y' = 3{x^2} + 8x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = \dfrac{1}{3}\end{array} \right.\)
BBT:
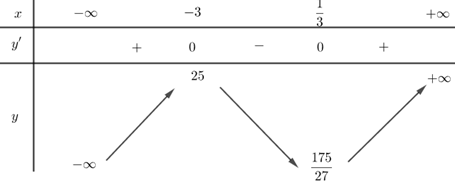
Từ BBT ta thấy \(x = \dfrac{1}{3}\) là điểm cực tiểu của hàm số đã cho.
Chọn D.
Câu hỏi trước
