Phương pháp giải:

Công thức độc lập với thời gian: \({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2}\)

Sử dụng vòng tròn lượng giác và công thức: \(\Delta \varphi  = \omega \Delta t\)

Lời giải chi tiết:

Vận tốc của vật bằng một nửa vận tốc cực đại, ta có:

\({x^2} + \dfrac{{{v_{\max }}^2}}{{4{\omega ^2}}} = {A^2} \Rightarrow {x^2} + \dfrac{{{A^2}{\omega ^2}}}{{4{\omega ^2}}} = {A^2} \Rightarrow x = \dfrac{{A\sqrt 3 }}{2}\)

Ta có vòng tròn lượng giác:

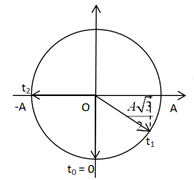
Từ vòng tròn lượng giác, ta thấy từ thời điểm t₀ đến t₁, vecto quay được góc: \(\Delta \varphi  = \dfrac{\pi }{3}\,\,\left( {rad} \right)\)

Ta có: \(\omega  = \dfrac{{\Delta \varphi }}{{\Delta t}} = \dfrac{{\dfrac{\pi }{3}}}{{\dfrac{\pi }{{15}}}} = 5\,\,\left( {rad/s} \right)\)

Từ thời điểm t₀ đến t₂, quãng đường vật đi được là:

\(3A = 12 \Rightarrow A = 4\,\,\left( {cm} \right)\)

Vận tốc của vật ở thời điểm t₀ là: \({v_{\max }} = \omega A = 5.4 = 20\,\,\left( {cm/s} \right)\)

Chọn C.