Phương pháp giải:

Sử dụng vòng tròn lượng giác, công thức độc lập với thời gian \({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\) và tốc độ trung bình \({v_{tb}} = \frac{s}{{\Delta t}}\)

Lời giải chi tiết:

Ta có tốc độ trung bình của vật trong 1 chu kì:

\({v_{tb}} = \frac{s}{t} = \frac{{4A}}{T} = \frac{{4A}}{{\frac{{2\pi }}{\omega }}} = \frac{{2A\omega }}{\pi }\)

Vận tốc tức thời: \(v \ge \frac{\pi }{4}{v_{tb}} \Rightarrow v \ge \frac{{A\omega }}{2}\)

Áp dụng công thức độc lập với thời gian, ta có:

\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow {v^2} = {\omega ^2}\left( {{A^2} - {x^2}} \right)\)

Mà:

\(\begin{gathered}
v \geqslant \frac{{A\omega }}{2} \Leftrightarrow {v^2} \geqslant \frac{{{A^2}{\omega ^2}}}{4} \Leftrightarrow {\omega ^2}\left( {{A^2} - {x^2}} \right) \geqslant \frac{{{A^2}{\omega ^2}}}{4} \hfill \\
\Leftrightarrow {A^2} - {x^2} \geqslant \frac{{{A^2}}}{4} \Rightarrow {x^2} \leqslant \frac{{3{A^2}}}{4} \Rightarrow \frac{{ - A\sqrt 3 }}{2} \leqslant x \leqslant \frac{{A\sqrt 3 }}{2} \hfill \\
\end{gathered} \)

Biểu diễn trên VTLG, ta có:

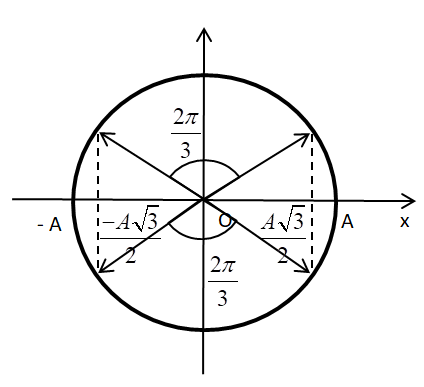
Từ VTLG, ta thấy khoảng thời gian vật có độ lớn vận tốc tức thời không nhỏ hơn \(\frac{\pi }{4}\) lần tốc độ trung bình trong 1 chu kỳ là

\(\Delta t = \frac{{\Delta \varphi }}{\omega } = \frac{{2.\frac{{2\pi }}{3}}}{{\frac{{2\pi }}{T}}} = \frac{{2T}}{3}\)

Chọn C.