Phương pháp giải:

Tìm tâm \(I\) của mặt cầu ngoại tiếp hình chóp \(S.ABCD\) bằng cách :

- Tìm tâm \(O\) của đường tròn ngoại tiếp đa giác đáy \(ABCD\).

- Dựng đường thẳng \(d\) qua \(O\) và vuông góc với \(\left( {ABCD} \right).\)

- \(I\) là giao điểm của \(d\) và mặt phẳng trung trực bất kì của cạnh bên.

Tính bán kính của mặt cầu ngoại tiếp hình chóp

Lời giải chi tiết:

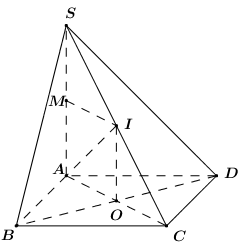
Gọi \(O = AC \cap BD \Rightarrow O\) là tâm đường tròn ngoại tiếp hình vuông \(ABCD\).

Dựng đường thẳng \(d\) qua \(O\) và vuông góc với \(\left( {ABCD} \right).\)

Dựng mặt phẳng \(\left( \alpha  \right)\) là mặt phẳng trung trực của cạnh bên \(SA\) và cắt \(SA\) tại \(M\).

Gọi \(I = d \cap \left( \alpha  \right)\) là tâm mặt cầu ngoại tiếp khối chóp \(S.ABCD.\)

Ta có : \({V_{S.ABCD}} = \dfrac{1}{3}SA.A{B^2} \Leftrightarrow \dfrac{{\sqrt 2 }}{3}{a^3} = \dfrac{1}{2}.a\sqrt 2 .A{B^2} \Rightarrow AB = a\)

\( \Rightarrow AD = a\sqrt 2  \Rightarrow AO = \dfrac{{a\sqrt 2 }}{2}\).

Do \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Leftrightarrow MA \bot AO\).

Ta có \(SA = a\sqrt 2  \Rightarrow AM = \dfrac{{a\sqrt 2 }}{2} = OI\).

Áp dụng định lí Pytago trong tam giác vuông \(OAI\) có:

\(R = AI = \sqrt {A{O^2} + O{I^2}}  = \sqrt {{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}}  = a\).

Chọn C.