Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy là hình thang vuông tại \(A\) và \(B\), \(SA \bot \left( {ABCD} \right)\), \(AD > BC\). Xác định tâm \(I\) của mặt cầu ngoại tiếp hình chóp \(S.ABCD\).
- A \(I\) là trung điểm của cạnh \(SC\).
- B \(I\) là trung điểm của cạnh \(SB\).
- C \(I\) không tồn tại.
- D \(I\) là trọng tâm của tam giác \(SAC\).
Phương pháp giải:
Khối chóp có mặt cầu ngoại tiếp khi và chỉ khi tất cả các mặt của chóp là đa giác nội tiếp.
Lời giải chi tiết:
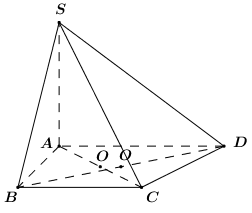
Giả sử có đường tròn ngoại tiếp hình thang \(ABCD\).
Gọi \(O\) là tâm đường tròn ngoại tiếp đáy \( \Rightarrow OA = OB = OC = OD\).
\(OA = OB = OD \Rightarrow O\) là tâm đường tròn ngoại tiếp \(\Delta ABD \Rightarrow O\) là trung điểm của \(BD\) (do tam giác \(ABD\) vuông tại \(A\))
CMTT ta có \(O\) là trung điểm của \(AC\).
Khi đó \(ABCD\) là hình bình hành, lại có \(\angle BAD = {90^0} \Rightarrow ABCD\) là hình chữ nhật.
\( \Rightarrow AD = BC\) (mâu thuẫn).
Vậy không có mặt cầu ngoại tiếp chóp \(S.ABCD\) hay không tồn tại tâm \(I\) của mặt cầu ngoại tiếp hình chóp \(S.ABCD\).
Chọn C.







