Phương pháp giải:

- Xác định tâm mặt cầu ngoại tiếp của hình lăng trụ và bán kính \(R\) của mặt cầu đó.

- Diện tích mặt cầu ngoại tiếp là \(S = 4\pi {R^2}.\)

Lời giải chi tiết:

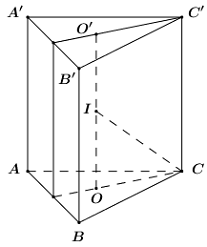
Gọi hình lăng trụ đã cho là \(ABC.A'B'C'\).

Hình lăng trụ đã cho là hình lăng trụ tam giác đều nên tâm mặt cầu ngoại tiếp lăng trụ là trung điểm đoạn nối tâm 2 đáy.

Gọi \(O\) và \(O'\) lần lượt là tâm của hai đáy \(ABC\) và \(A'B'C'\).

Gọi \(I\) là trung điểm \(OO'\) suy ra \(I\) là tâm mặt cầu ngoại tiếp lăng trụ \(ABC.A'B'C'\)

Ta có: \(R = IC = \sqrt {I{O^2} + O{C^2}} \)

\(\left\{ \begin{array}{l}IO = \dfrac{1}{2}OO' = \dfrac{1}{2}AA' = \dfrac{a}{2}\\OA = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\end{array} \right. \Rightarrow R = \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}}  = \dfrac{{a\sqrt {21} }}{6}.\)

Vậy diện tích mặt cầu ngoại tiếp hình lăng trụ đó là \(S = 4\pi {R^2} = \dfrac{{7\pi {a^2}}}{3}.\)

Chọn B.