Câu hỏi
Cho điểm \(A\) nằm ngoài mặt cầu \(S\left( {O;R} \right)\). Biết rằng qua \(A\) có vô số tiếp tuyến với mặt cầu. Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu có bán kính bằng \(\dfrac{{\sqrt 2 }}{2}R\). Tính độ dài đoạn thẳng \(OA\) theo \(R.\)
- A \(\sqrt 3 R\)
- B \(\sqrt 2 R\)
- C \(2R\)
- D \(\dfrac{{\sqrt 2 }}{2}R\)
Phương pháp giải:
Vẽ hình và phân tích đề
Vận dụng các kiến thức về hình học để tính
Lời giải chi tiết:
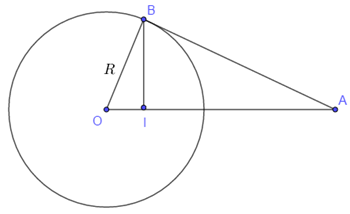
Giả sử có một tiếp tuyến đi qua \(A\) và cắt mặt cầu tại \(B\).
Qua \(B\) kẻ \(BI \bot OA\,\,\,\left( {I \in OA} \right)\) thì \(I\) là tâm đường tròn là tập hợp các tiếp điểm của tiếp tuyến kẻ từ \(A\).
Theo giả thiết ta có: \(IB = \dfrac{{\sqrt 2 R}}{2}\).
Tam giác \(OBA\) vuông tại \(B\), có chiều cao \(BI\) nên ta có:
\(\dfrac{1}{{I{B^2}}} = \dfrac{1}{{O{B^2}}} + \dfrac{1}{{B{A^2}}}\) (hệ thức lượng trong tam giác vuông).
\(\begin{array}{l} \Leftrightarrow \dfrac{1}{{{{\left( {\dfrac{{\sqrt 2 R}}{2}} \right)}^2}}} = \dfrac{1}{{{R^2}}} + \dfrac{1}{{B{A^2}}} \Rightarrow BA = R\\ \Rightarrow OA = \sqrt {O{B^2} + B{A^2}} = \sqrt 2 R\end{array}\)
Chọn B.







