Phương pháp giải:

Hàm số \(y = f\left( x \right)\) có \(f'\left( x \right) < 0\,\,\forall x \in \mathbb{R}\) là hàm nghịch biến trên \(\mathbb{R}\). Khi đó \(f\left( {{x_1}} \right) = f\left( {{x_2}} \right) \Leftrightarrow {x_1} = {x_2}.\)

Lời giải chi tiết:

Hàm số đã cho có \(f'\left( x \right) < 0\,\,\forall x \in \mathbb{R} \Rightarrow \) Hàm số nghịch biến trên \(\mathbb{R}\).

Do đó:

\(\begin{array}{l}f\left( {\sin x + \cos 2x} \right) = f\left( m \right) \Leftrightarrow \sin x + \cos 2x = m\\ \Leftrightarrow \sin x + 1 - 2{\sin ^2}x = m \Leftrightarrow  - 2{\sin ^2}x + \sin x + 1 = m\end{array}\)

Đặt \(t = \sin x\,\,\,\left( {t \in \left[ { - 1;1} \right]} \right)\) thì ta có : \(m =  - 2{t^2} + t + 1 = g\left( t \right)\,\,\,\left( 1 \right).\)

Để phương trình đã cho có nghiệm với \(\forall x \in \mathbb{R}\) thì phương trình (1) phải có nghiệm với mọi \(t \in \left[ { - 1;1} \right].\)

Xét hàm số \(g\left( t \right) =  - 2{t^2} + t + 1\) trên \(\left[ { - 1;1} \right]\) ta có : \(g'\left( t \right) =  - 4t + 1 = 0 \Leftrightarrow t = \dfrac{1}{4}\)

BBT:

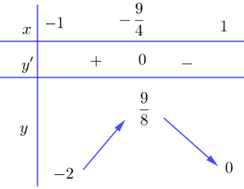
Từ BBT ta thấy, để phương trình (1) có nghiệm với  mọi \(t \in \left[ { - 1;1} \right]\) thì  \(m \in \left[ { - 2;\dfrac{9}{8}} \right].\)

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2; - 1;0;1} \right\}.\)

Vậy có 4 giá trị nguyên của \(m\) thỏa mãn.

Chọn B.