Phương pháp giải:

1) Sử dụng định nghĩa về hàm số chẵn, lẻ.

2) Lập bảng biến thiên và vẽ đồ thị như sách giáo khoa.

3) Thay tọa độ các điểm vào hàm số, sử dụng công thực tọa độ đỉnh.

Lời giải chi tiết:

1) Xét tính chẵn, lẻ của hàm số \(f\left( x \right) = {x^4} - 3{x^2} + 2.\)

Tập xác định : \(D = \mathbb{R}.\)

\( \Rightarrow \forall \,\,x \in D \Rightarrow  - x \in D.\)

Xét \(f\left( { - x} \right) = {\left( { - x} \right)^4} - 3{\left( { - x} \right)^2} + 2 = {x^4} - 3{x^2} + 2 \Rightarrow f\left( x \right) = f\left( { - x} \right).\)

Vậy \(f\left( x \right)\) là hàm số chẵn.

2) Lập bảng biến thiên và vẽ đồ thị hàm số : \(y = {x^2} + 2x - 3.\)

Tập xác định : \(D = \mathbb{R}.\)

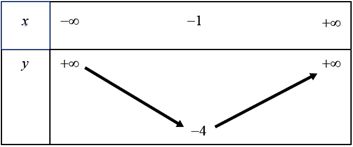
Bảng biến thiên:

Đồ thị hàm số có đỉnh \(I\left( { - 1; - 4} \right)\) và nhận đường thẳng \(x =  - 1\) làm trục đối xứng.

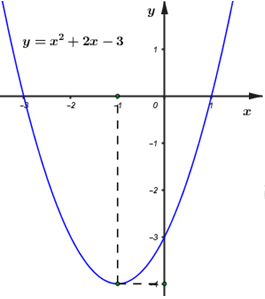
Đồ thị hàm số:

3) Xác định \(a,\,\,b,\,\,c\) để parabol \(\left( P \right):\,\,y = a{x^2} + bx + c\) đi qua điểm \(A\left( {2;\,\,1} \right)\) và có đỉnh \(I\left( {1; - 1} \right).\)

Parabol đi qua điểm \(A\left( {2;1} \right)\) và có đỉnh \(I\left( {1; - 1} \right)\)

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}a{.2^2} + b.2 + c = 1\\\frac{{ - b}}{{2a}} = 1\\\frac{{ - \left( {{b^2} - 4ac} \right)}}{{4a}} =  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + 2b + c = 1\\2a + b = 0\\{b^2} - 4ac - 4a = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + 2b + c = 1\\b =  - 2a\\{\left( { - 2a} \right)^2} - 4ac - 4a = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4a + 2b + c = 1\\b =  - 2a\\4a\left( {a - c - 1} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + 2b + c = 1\\2a + b = 0\\a - c = 1\,\,\,\left( {do\,\,\,a \ne 0} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b =  - 4\\c = 1\end{array} \right..\end{array}\)

Vậy \(a = 2,b =  - 4,c = 1.\)

Chọn A.