Phương pháp giải:

Dùng bảng biến thiên tìm giá trị lớn nhất của hàm số.

Lời giải chi tiết:

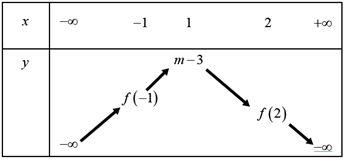
Xét hàm số: \(y =  - {x^2} + 2x + m - 4\) ta có tọa độ đỉnh của đồ thị hàm số là: \(I\left( {1;\,\,m - 3} \right)\)

Ta có BBT:

Từ bảng biến thiên suy ra giá trị lớn nhất của hàm số trên \(\left[ { - 1;2} \right]\) là \(m - 3.\)

Giá trị lớn nhất của hàm số trên \(\left[ { - 1;2} \right]\) bằng  \(3 \Leftrightarrow m - 3 = 3 \Leftrightarrow m = 6.\)

\( \Rightarrow m \in \left( {5;\,\,7} \right).\)

Chọn C.