Phương pháp giải:

Xác định được tâm mặt cầu ngoại tiếp hình chóp

- Xác định trục \(d\) của mặt đáy.

- Xác định mặt phẳng trung trực \(\left( P \right)\) của 1 cạnh bên.

- Xác định giao điểm của \(d\) và \(\left( P \right)\), đó chính là tâm mặt cầu ngoại tiếp chóp

Lời giải chi tiết:

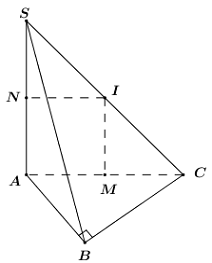
Gọi \(M,\,\,N,\,\,I\) lần lượt là trung điểm của \(AC,\,\,SA,\,\,SC\).

Tam giác \(ABC\) vuông tại \(B \Rightarrow M\) là tâm đường tròn ngoại tiếp \(\Delta ABC\).

Lại có \(IM\) là đường trung bình của tam giác \(SAC \Rightarrow IM\parallel SA \Rightarrow IM \bot \left( {ABC} \right)\).

\( \Rightarrow IA = IB = IC\,\,\left( 1 \right)\).

\(IN\) là đường trung bình của tam giác \(SAC \Rightarrow IN\parallel AC\).

Mà \(AC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right) \Rightarrow IN \bot SA \Rightarrow IN\) là đường trung trực của \(SA\).

\( \Rightarrow IS = IA\,\,\left( 2 \right)\) .

Từ (1) và (2) \( \Rightarrow IA = IB = IC = IS \Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\), bán kính mặt cầu là \(R = IS = \dfrac{{SC}}{2}\).

Áp dụng định lí Pytago ta có:

\(\begin{array}{l}AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {4{a^2} + 16{a^2}}  = \sqrt {20{a^2}} \\SC = \sqrt {S{A^2} + A{C^2}}  = \sqrt {16{a^2} + 20{a^2}}  = 6a\end{array}\)

Vậy \(R = \dfrac{1}{2}SC = 3a\).

Chọn A.