Phương pháp giải:

Tìm điểm cách đều 8 điểm đã cho rồi từ đó tính bán kính mặt cầu.

Lời giải chi tiết:

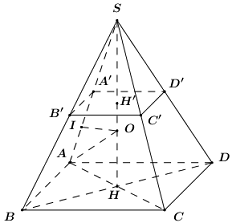
Gọi \(H\) là tâm của hình vuông \(ABCD \Rightarrow SH\) là trục của hình vuông \(ABCD\).

Gọi \(H' = SO \cap \left( {A'B'C'D'} \right)\), dễ dàng chứng minh được \(H'\) là tâm hình vuông \(A'B'C'D'\), do đó \(SH\) cũng chính là trục của hình vuông \(A'B'C'D'\).

Trên \(SH\) lấy \(O\)sao cho \(OA = OA'\) ta có:

\(O \in SH \Rightarrow \left\{ \begin{array}{l}OA = OB = OC = OD\\OA' = OB' = OC' = OD'\end{array} \right.\).

Vậy \(O\) là tâm mặt cầu cần tìm.

Gọi \(I\)là trung điểm của \(AA' \Rightarrow IO \bot AA'.\)

Vì tất cả các cạnh của hình chóp đều bằng \(a \Rightarrow A{C^2} = 2{a^2} = S{A^2} + S{C^2}\)

Nên \(\Delta SAC\)vuông cân tại\(S \Rightarrow SH = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)

Ta có: \(\Delta SIO \sim \Delta SHA\,\,\left( {g.g} \right) \Rightarrow \dfrac{{SI}}{{SH}} = \dfrac{{OI}}{{AH}}\).

\( \Rightarrow OI = \dfrac{{SI.AH}}{{SH}} = \dfrac{{\dfrac{3}{4}a.\dfrac{{a\sqrt 2 }}{2}}}{{\dfrac{{a\sqrt 2 }}{2}}} = \dfrac{3}{4}a.\)

\( \Rightarrow AO = \sqrt {A'{I^2} + I{O^2}}  = \sqrt {{{\left( {\dfrac{a}{4}} \right)}^2} + {{\left( {\dfrac{3}{4}a} \right)}^2}}  = \dfrac{{a\sqrt {10} }}{4}.\)

Chọn C