 Môn Lý - Lớp 12
Môn Lý - Lớp 12
 50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng (Phần 2)
50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng (Phần 2)
Câu hỏi
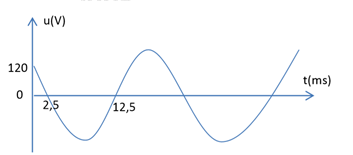
Cho đồ thị phụ thuộc thời gian của điện áp xoay chiều như hình vẽ. Đặt điện áp đó vào hai đầu đoạn mạch gồm một cuộn dây thuần cảm L, điện trở thuần R, tụ điện \({\rm{C = }}\dfrac{{\rm{1}}}{{{\rm{2\pi }}}}{\rm{ mF}}\) mắc nối tiếp. Biết hiệu điện thế hiệu dụng hai đầu cuộn dây L và hai đầu tụ điện bằng nhau và bằng một nửa trên điện trở R. Công suất tiêu thụ trên đoạn mạch đó là
- A 360W
- B 560W
- C 180W
- D 720W
Phương pháp giải:
Từ đồ thị, vẽ vòng tròn lượng giác để xác định tần số góc và điện áp cực đại giữa hai đầu đoạn mạch.
Công suất tiêu thụ trên đoạn mạch: \({\rm{P = UI = }}{{\rm{I}}^{\rm{2}}}{\rm{R = }}\dfrac{{{{\rm{U}}_{\rm{R}}}^{\rm{2}}}}{{\rm{R}}}\)
Lời giải chi tiết:
Từ đồ thị, ta thấy chu kì của điện áp hai đầu đoạn mạch là:
\(\begin{gathered}
{\text{T = 2}}.\left( {{\text{12}},{\text{5}} - {\text{2}},{\text{5}}} \right).{\text{1}}{{\text{0}}^{ - {\text{3}}}}{\text{ = 0}},{\text{02}}\left( {\text{s}} \right) \hfill \\
\Rightarrow \omega {\text{ = }}\frac{{{\text{2}}\pi }}{{\text{T}}}{\text{ = }}\frac{{{\text{2}}\pi }}{{{\text{0}},{\text{02}}}}{\text{ = 100}}\pi \left( {{\text{rad/s}}} \right) \hfill \\
\end{gathered} \)
Ở thời điểm \({\rm{t = 2,5}}{\rm{.1}}{{\rm{0}}^{ - {\rm{3}}}}{\rm{ s}}\), điện áp bằng 0 và đang giảm, góc quay của điện áp là:
\({\rm{\Delta \varphi = \omega \Delta t = 100\pi }}{\rm{.2,5}}{\rm{.1}}{{\rm{0}}^{ - {\rm{3}}}}{\rm{ = }}\dfrac{{\rm{\pi }}}{{\rm{4}}}\,\,\left( {{\rm{rad}}} \right)\)
Ta có vòng tròn lượng giác:
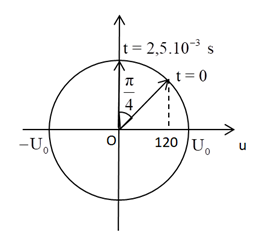
Từ vòng tròn lượng giác, ta thấy:
\({\rm{120 = }}{{\rm{U}}_{\rm{0}}}{\rm{cos}}\dfrac{{\rm{\pi }}}{{\rm{4}}} \Rightarrow {{\rm{U}}_{\rm{0}}}{\rm{ = 120}}\sqrt {\rm{2}} \,\,\left( {\rm{V}} \right)\)
Theo đề bài ta có:
\({{\text{U}}_{\text{L}}}{\text{ = }}{{\text{U}}_{\text{C}}}{\text{ = }}\frac{{{{\text{U}}_{\text{R}}}}}{{\text{2}}} \Rightarrow {\text{I}}.{{\text{Z}}_{\text{L}}}{\text{ = I}}.{{\text{Z}}_{\text{C}}}{\text{ = }}\frac{{{\text{I}}.{\text{R}}}}{{\text{2}}}\)
\( \Rightarrow {{\text{Z}}_{\text{L}}}{\text{ = }}{{\text{Z}}_{\text{C}}}{\text{ = }}\frac{{\text{R}}}{{\text{2}}} \Rightarrow \) trong mạch có cộng hưởng.
\( \Rightarrow \left\{ \begin{array}{l}{\rm{\omega = }}\dfrac{{\rm{1}}}{{\sqrt {{\rm{LC}}} }} \Rightarrow {\rm{L = }}\dfrac{{\rm{1}}}{{{{\rm{\omega }}^{\rm{2}}}{\rm{C}}}}{\rm{ = }}\dfrac{{\rm{1}}}{{{{\left( {{\rm{100\pi }}} \right)}^{\rm{2}}}{\rm{.}}\dfrac{{{\rm{1}}{{\rm{0}}^{ - {\rm{3}}}}}}{{{\rm{2\pi }}}}}}{\rm{ = }}\dfrac{{{\rm{0,2}}}}{{\rm{\pi }}}\,\,\left( {\rm{H}} \right)\\{{\rm{U}}_{\rm{R}}}{\rm{ = U = }}\dfrac{{{{\rm{U}}_{\rm{0}}}}}{{\sqrt {\rm{2}} }}{\rm{ = }}\dfrac{{{\rm{120}}\sqrt {\rm{2}} }}{{\sqrt {\rm{2}} }}{\rm{ = 120}}\,\,\left( {\rm{V}} \right)\end{array} \right.\)
Dung kháng của tụ điện là:
\(\begin{gathered}
{{\text{Z}}_{\text{C}}}{\text{ = }}\frac{{\text{1}}}{{\omega {\text{C}}}}{\text{ = }}\frac{{\text{1}}}{{{\text{100}}\pi .\frac{{{\text{1}}{{\text{0}}^{ - {\text{3}}}}}}{{{\text{2}}\pi }}}}{\text{ = 20}}{\mkern 1mu} {\mkern 1mu} \left( \Omega \right) \hfill \\
\Rightarrow {\text{R = 2}}{{\text{Z}}_{\text{C}}}{\text{ = 2}}.{\text{20 = 40}}\,\,\left( \Omega \right) \hfill \\
\end{gathered} \)
Công suất của mạch là:
\({\rm{P = }}\dfrac{{{{\rm{U}}_{\rm{R}}}^{\rm{2}}}}{{\rm{R}}}{\rm{ = }}\dfrac{{{\rm{12}}{{\rm{0}}^{\rm{2}}}}}{{{\rm{40}}}}{\rm{ = 360}}\,\,\left( {\rm{W}} \right)\)
Chọn A.






