Câu hỏi
Khối hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a\), \(AD = a\sqrt 3 \), \(AC' = a\sqrt 6 \) có thể tích là:
- A \(\dfrac{{{a^3}\sqrt 6 }}{3}\)
- B \({a^3}\sqrt 6 \)
- C \(\dfrac{{2{a^3}\sqrt 6 }}{3}\)
- D \(3{a^3}\sqrt 2 \)
Phương pháp giải:
Hình hộp chữ nhật có kích thước \(a \times b \times c\) có thể tích \(V = a.b.c\).
Lời giải chi tiết:
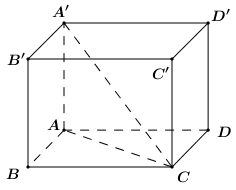
Áp dụng định lí Pytago ta có:
\(\begin{array}{l}AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + 3{a^2}} = 2a\\AA' = \sqrt {AC{'^2} - A{C^2}} = \sqrt {6{a^2} - 4{a^2}} = a\sqrt 2 \end{array}\)
Vậy thể tích khối hộp hình hộp chữ nhật là \(V = a.a\sqrt 3 .a\sqrt 2 = {a^3}\sqrt 6 .\)
Chọn B.
Câu hỏi trước
