Phương pháp giải:

Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {a;b} \right) \Leftrightarrow f'\left( x \right) < 0\,\,\forall x \in \left( {a;b} \right)\) và bằng 0 tại hữu hạn điểm.

Lời giải chi tiết:

Hàm số \(y =  - {x^3} - 3{x^2} + mx + 4\) có đạo hàm \(y' =  - 3{x^2} - 6x + m\)

Hàm số đã cho nghịch biến trên \(\left( {0; + \infty } \right)\) khi \(y' =  - 3{x^2} - 6x + m < 0\,\,\forall x \in \left( {0; + \infty } \right)\)

Ta có : \(y' < 0 \Leftrightarrow m < 3{x^2} + 6x\,\,\forall x \in \left( {0; + \infty } \right)\,\,\,\left( * \right)\)

Đặt \(g\left( x \right) = 3{x^2} + 6x \Rightarrow g'\left( x \right) = 6x + 6 = 0 \Leftrightarrow x =  - 1\)

Ta có bảng biến thiên:

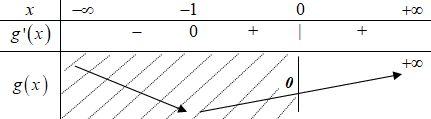
Dựa vào bảng biến thiên ta có bất đẳng thức (*) thỏa mãn khi \(m < 0\).

Kết hợp điều kiện \( \Rightarrow m \in \left( { - 21;0} \right),\,\,m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 20; - 19;...; - 2; - 1} \right\}\).

Vậy \(S =  - \dfrac{{20.21}}{2} =  - 210\).

Chọn A