Câu hỏi
Tìm các giá trị của m để phương trình \({x^3} - 6{x^2} + 9x - 3 - m = 0\) có ba nghiệm thực phân biệt trình đó hai nghiệm lớn hơn 2.
- A \( - 3 < m < - 1.\)
- B \(1 < m < 3.\)
- C \( - 1 < m < 1.\)
- D \( - 3 < m < 1.\)
Phương pháp giải:
Cô lập \(m\). Lập BBT và kết luận.
Lời giải chi tiết:
\({x^3} - 6{x^2} + 9x - 3 - m = 0 \Leftrightarrow {x^3} - 6{x^2} + 9x - 3 = m\).
Đặt \(f\left( x \right) = {x^3} - 6{x^2} + 9x - 3\) ta có: \(f'\left( x \right) = 3{x^2} - 12x + 9 = 3\left( {x - 3} \right)\left( {x - 1} \right)\).
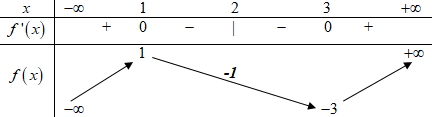
Dựa vào bảng biến thiên ta thấy phương trình đã cho có 3 nghiệm thực phân biệt trong đó hai nghiệm lớn hơn 2 khi \( - 3 < m < - 1.\)
Chọn A
Câu hỏi trước
