Phương pháp giải:

+ Chứng minh \(A'O \bot \left( {BDD'B'} \right)\).

+ Tính thể tích khối chóp \(A.BDD'B'\) theo \(a\).

Lời giải chi tiết:

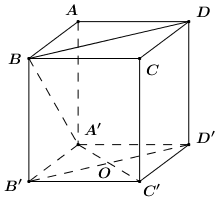
Gọi \(O = A'C \cap B'D'\).

Vì \(A'B'C'D'\) là hình vuông nên \(A'C' \bot B'D' \Rightarrow A'O \bot B'D'\).

Lại có \(BB' \bot A'O\,\,\left( {BB' \bot \left( {A'B'C'D'} \right)} \right)\).

\( \Rightarrow A'O \bot \left( {BDD'B'} \right)\).

Khi đó ta có:

\({V_{A'BDD'B'}} = \dfrac{1}{3}.A'O.{S_{BDD'B'}} = \dfrac{1}{3}.A'O.BD.BB' = \dfrac{1}{3}.\dfrac{{a\sqrt 2 }}{2}.a\sqrt 2 .a = \dfrac{{{a^3}}}{3}.\)

\( \Rightarrow \dfrac{8}{3} = \dfrac{{{a^3}}}{3} \Leftrightarrow {a^3} = 8 \Leftrightarrow a = 2\,\,\left( {dm} \right).\)

Chọn D