Phương pháp giải:

+ Trong \(\left( ABD \right)\), từ \(B\) dựng đường thẳng vuông góc  với \(AB\) cắt \(AD\) ở \(E\). Tính thể tích khối tứ diện \(ABCE\).

+ Sử dụng tỉ lệ thể tích.

Lời giải chi tiết:

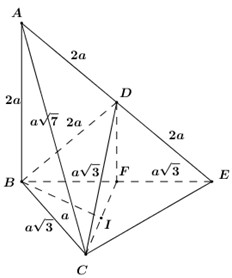
Trong \(\left( {ABD} \right)\), từ \(B\) dựng đường thẳng vuông góc  với \(AB\) cắt \(AD\) ở \(E\) (như hình vẽ).

Xét tam giác \(ABC\) ta có:

\(A{B^2} + B{C^2} = {\left( {2a} \right)^2} + {\left( {a\sqrt 3 } \right)^2} = 7{a^2} = A{C^2} \Rightarrow \Delta ABC\) vuông tại \(B\).

\( \Rightarrow AB \bot BC\). Lại có \(AB \bot BE \Rightarrow AB \bot \left( {BCF} \right)\).

Tam giác \(ABD\) đều \( \Rightarrow \angle BAD = {60^0}\).

Xét tam giác vuông \(ABE\) có:

\(AE = \dfrac{{AB}}{{\cos {{60}^0}}} = 4a;\,\,BE = AB.\tan {60^0} = 2\sqrt 3 a\).

\( \Rightarrow DE = AE - AD = 4a - 2a = 2a = AD \Rightarrow D\) là trung điểm của \(AE\).

Gọi \(F\) là trung điểm của \(BE\) \( \Rightarrow BF = EF = a\sqrt 3  = BC\).

\( \Rightarrow DF\) là đường trung bình của tam giác \(ABE \Rightarrow DF\parallel AB\).

Mà \(AB \bot \left( {BCE} \right) \Rightarrow DF \bot \left( {BCE} \right)\).

Gọi \(I\) là trung điểm của \(CF\). Tam giác \(BCF\) cân tại \(B \Rightarrow BI \bot CF\).

Mà \(DF \bot \left( {BCE} \right) \Rightarrow DF \bot BI \Rightarrow BI \bot \left( {CDF} \right)\).

Ta có: \(AB\parallel \left( {CDF} \right) \supset CD \Rightarrow d\left( {AB;CD} \right) = d\left( {AB;\left( {CDF} \right)} \right) = d\left( {B;\left( {CDF} \right)} \right) = BI = a\).

Xét tam giác vuong \(BCI\) có: \(CI = \sqrt {B{C^2} - B{I^2}}  = \sqrt {3{a^2} - {a^2}}  = a\sqrt 2  \Rightarrow CF = 2CI = 2\sqrt 2 a\).

Ta có \({S_{BCF}} = \dfrac{1}{2}BI.CF = \dfrac{1}{2}.a.2\sqrt 2 a = {a^2}\sqrt 2 \).

\(\dfrac{{{S_{BCE}}}}{{{S_{BCF}}}} = \dfrac{{\dfrac{1}{2}.d\left( {C;BE} \right).BE}}{{\dfrac{1}{2}d\left( {C;BE} \right).BF}} = 2 \Rightarrow {S_{BCE}} = 2{S_{BCF}} = 2{a^2}\sqrt 2 \).

\( \Rightarrow {V_{ABCE}} = \dfrac{1}{3}AB.{S_{BCE}} = \dfrac{1}{3}.2a.2{a^2}\sqrt 2  = \dfrac{{4{a^3}\sqrt 2 }}{3}\).

Ta có: \(\dfrac{{{V_{ABCD}}}}{{{V_{ABCE}}}} = \dfrac{{AD}}{{AE}} = \dfrac{1}{2} \Rightarrow {V_{ABCD}} = \dfrac{1}{2}{V_{ABCE}} = \dfrac{1}{2}.\dfrac{{4{a^3}\sqrt 2 }}{3} = \dfrac{{2{a^3}\sqrt 2 }}{3}\).

Chọn B.