Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(f\left( 0 \right) = 0;{\rm{ }}f\left( 4 \right) > 4\). Biết đồ thị hàm \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên. Tìm số điểm cực trị của hàm số \(g\left( x \right) = \left| {f\left( {{x^2}} \right) - 2x} \right|\).
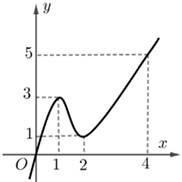
- A \(1\)
- B \(2\)
- C \(5\)
- D \(3\)
Lời giải chi tiết:
Đặt \(h\left( x \right) = f\left( {{x^2}} \right) - 2x\) ta có \(h'\left( x \right) = 2xf'\left( {{x^2}} \right) - 2 = 2\left[ {xf'\left( {{x^2}} \right) - 1} \right]\).
+ Với \(x \le 0 \Rightarrow {x^2} \ge 0 \Rightarrow f'\left( {{x^2}} \right) \ge 0\).
\( \Rightarrow xf'\left( {{x^2}} \right) \le 0 \Leftrightarrow {x^2}f'\left( {{x^2}} \right) - 1 < 0 \Leftrightarrow h'\left( x \right) < 0\,\,\forall x \le 0\).
+ Với \(x > 0\) ta có: \(h'\left( x \right) = 0 \Leftrightarrow xf'\left( {{x^2}} \right) - 1 = 0 \Leftrightarrow f'\left( {{x^2}} \right) = \dfrac{1}{x} = \dfrac{1}{{\sqrt {{x^2}} }}\).
Đặt \(t = {x^2}\,\,\left( {t > 0} \right)\) ta có \(f'\left( t \right) = \dfrac{1}{{\sqrt t }} \Rightarrow \) Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f'\left( t \right)\) và \(y = \dfrac{1}{{\sqrt x }}\). Ta có đồ thị hàm số như sau:
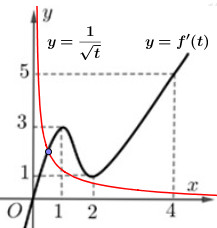
Dựa vào đồ thị hàm số ta thấy \(f'\left( t \right) = \dfrac{1}{{\sqrt t }} \Leftrightarrow t = {t_0} \in \left( {0;1} \right) \Rightarrow x = \sqrt {{t_0}} \in \left( {0;1} \right)\). Ta có BBT:
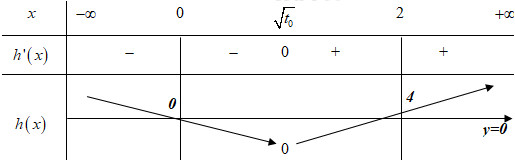
Ta có: \(h\left( 0 \right) = f\left( 0 \right) - 0 = 0;\,\,h\left( 2 \right) = f\left( 4 \right) - 4 > 0\).
Dựa vào BBT ta thấy đồ thị hàm số \(y = \left| {h\left( x \right)} \right|\) sẽ có 3 điểm cực trị.
Chọn D.







