Phương pháp giải:

Lập BBT của hàm số và kết luận các khoảng đơn điệu của hàm số.

Lời giải chi tiết:

+ TXĐ: \(D = \left( { - \infty ; - 1} \right] \cup \left[ {5; + \infty } \right)\).

+ Ta có \(y' = \dfrac{{2x - 4}}{{2\sqrt {{x^2} - 4x - 5} }} = \dfrac{{x - 2}}{{\sqrt {{x^2} - 4x - 5} }}\).

+ Cho \(y' = 0 \Leftrightarrow x - 2 = 0 \Leftrightarrow x = 2 \notin D\).

+ BBT:

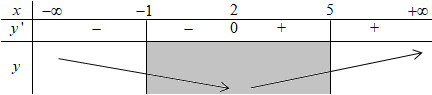
Từ BBT ta thấy hàm số đồng biến trên \(\left( {5; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - 1} \right)\).

Vậy khẳng định đúng là C.

Chọn C.