Phương pháp giải:

+ Đường thẳng \(x = a\) được gọi là TCĐ của đồ thị hàm số \(y = f\left( x \right) \Leftrightarrow \mathop {\lim }\limits_{x \to a} f\left( x \right) = \infty \).

+ Đường thẳng \(y = b\) được gọi là TCN của đồ thị hàm số \(y = f\left( x \right) \Leftrightarrow \mathop {\lim }\limits_{x \to  \pm \infty } f\left( x \right) = b.\)

Lời giải chi tiết:

Xét hàm số \(y = \dfrac{{2x + 1}}{{x - 1}}\)

TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}.\)

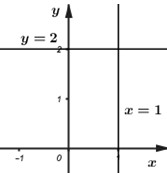
Đồ thì hàm số có TCĐ là: \(x = 1\)  và TCN là: \(y = 2.\)

\( \Rightarrow \) Hai đường tiệm cận của đồ thị hàm số tạo với hai trục tọa độ hình chữ nhật có diện tích là: \(S = 1.2 = 2.\)

Chọn A.