Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(1\). Mặt bên \(SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Hỏi bán kính \(R\) của mặt cầu ngoại tiếp hình chóp \(S.ABCD\) bằng bao nhiêu?
- A \(R = \dfrac{{\sqrt {11} }}{4}\)
- B \(R = \dfrac{1}{{\sqrt 3 }}\)
- C \(R = \dfrac{{\sqrt 7 }}{4}\)
- D \(R = \dfrac{{\sqrt {21} }}{6}\)
Lời giải chi tiết:
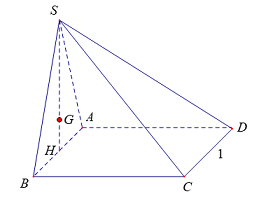
\( + )\) Gọi \(H\) là trung điểm \(AB \Rightarrow SH \bot \left( {ABCD} \right)\).
\( + )\)Xét \(\Delta SAB\)đều có: \(SH = \dfrac{{\sqrt 3 }}{2}.1 = \dfrac{{\sqrt 3 }}{2}\).
Gọi \(G\) là trọng tâm \(\Delta SAB \Rightarrow GS = HB = GA = \dfrac{2}{3}.SH = \dfrac{{\sqrt 3 }}{3}.\)
\( + )\) Xét hình vuông \(ABCD\):
Gọi \(O = AC \cap BD \Rightarrow OA = OB = OC = OD = \dfrac{{\sqrt 2 }}{2}\).
\( \Rightarrow R = \sqrt {G{S^2} + \dfrac{{A{B^2}}}{4}} = \sqrt {{{\left( {\dfrac{{\sqrt 3 }}{3}} \right)}^2} + \dfrac{1}{4}} = \dfrac{{\sqrt {21} }}{6}\)
Chọn D
Câu hỏi trước
