Lời giải chi tiết:

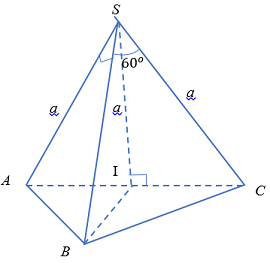
\( + )\)Xét \(\Delta SAB\) vuông tại \(S\)có: \(S{A^2} + S{B^2} = A{B^2}\)(Định lí Pytago)

\( \Leftrightarrow {a^2} + {a^2} = A{B^2} \Leftrightarrow AB = a\sqrt 2 \)

\( + )\)Xét \(\Delta SBC\) có: \(SB = SC = a,\,\,\widehat {BSC} = {60^0}\)

\( \Rightarrow \Delta SBC\)là tam giác đều cạnh \(a \Rightarrow BC = SB = SC = a\)

\( + )\)Xét \(\Delta SAC\)có:

\(\begin{array}{l}A{C^2} = S{A^2} + S{C^2} = 2SA.SC.cos\widehat {ASC}\\ \Leftrightarrow A{C^2} = {a^2} + {a^2} - 2{a^2}.\left( {\dfrac{{ - 1}}{2}} \right) = 3{a^2} \Leftrightarrow AC = a\sqrt 3 \end{array}\)

\( + )\)Xét \(\Delta ABC\)có: \(A{B^2} + B{C^2} = {\left( {a\sqrt 2 } \right)^2} + {a^2} = 3{a^2}\)

\(A{C^2} = {\left( {a\sqrt 3 } \right)^2} = 3{a^2} \Rightarrow A{B^2} + B{C^2} = A{C^2}\)

\( \Rightarrow \)\(\Delta ABC\) vuông tại \(B\) (Định lí Pytago đảo)

\( + )\)Xét \(\Delta ABC\) vuông tại \(B\): Gọi \(I\) là trung điểm \(AC\).

\( \Rightarrow BI = IA = IC = \dfrac{{AC}}{2} = \dfrac{{\sqrt 3 }}{2}a\)( tính chất trung điểm)

\( + )\) Vì \(S.ABC\) là hình chóp đều \(\left( {SA = SB = SC = a} \right)\)\( \Rightarrow SI \bot \left( {ABC} \right) \Rightarrow SI \bot IB.\)

\( + )\)Xét \(\Delta SIB\) vuông tại \(I\) có: \(S{I^2} + I{B^2} = S{B^2}\)(Định lí Pytago)

\( \Leftrightarrow S{I^2} = {a^2} - {\left( {\dfrac{{\sqrt 3 }}{2}a} \right)^2} \Leftrightarrow SI = \dfrac{a}{2}\)

\( \Rightarrow R = \dfrac{{S{A^2}}}{{2.SI}} = \dfrac{{{a^2}}}{{2.\dfrac{a}{2}}} = a \Rightarrow {S_{mc}} = 4\pi {R^2} = 4\pi {a^2}.\)

Chọn C