Câu hỏi
Cho hình chóp tam giác đều \(S.ABC\) có đáy bằng \(3a\), góc giữa cạnh bên và mặt đáy bằng \(45^\circ \). Thể tích khối cầu ngoại tiếp hình chóp \(S.ABC\) bằng
- A \(4\pi {a^3}\sqrt 2 \)
- B \(\dfrac{{4\pi {a^3}\sqrt 3 }}{3}\)
- C \(4\pi {a^3}\sqrt 3 \)
- D \(\dfrac{{4\pi {a^3}\sqrt 2 }}{3}\)
Lời giải chi tiết:
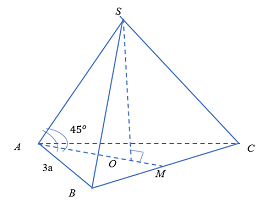
+ \(\widehat {\left( {SA;\left( {ABC} \right)} \right)} = {45^0}\).
\(A\) chung;
\(SO \bot \left( {ABC} \right)\) (\(O\)là trọng tâm \(\Delta ABC\))
\( \Rightarrow \widehat {\left( {SA;\left( {ABC} \right)} \right)} = \widehat {SAO} = {45^0}\).
\( + )\)Xét \(\Delta ABC\)đều:
Gọi \(M\) là trung điểm \(BC \Rightarrow AM = \dfrac{{\sqrt 3 }}{2}.3a = \dfrac{{3\sqrt 3 }}{2}a\).
\(O\) là trọng tâm \(\Delta ABC\)\( \Rightarrow \dfrac{{AO}}{{AM}} = \dfrac{2}{3}\)\( \Rightarrow AO = a\sqrt 3 \)
\( + )\)Xét \(\Delta SAO\)vuông tại \(O\) có:
\(\begin{array}{l}\tan \widehat {SAO} = \dfrac{{SO}}{{OA}} \Leftrightarrow \tan {45^0} = \dfrac{{SO}}{{a\sqrt 3 }} \Rightarrow SO = a\sqrt 3 \\\cos \widehat {SAO} = \dfrac{{OA}}{{SA}} \Leftrightarrow \cos {45^0} = \dfrac{{a\sqrt 3 }}{{SA}} \Rightarrow SA = a\sqrt 6 \\ \Rightarrow R = \dfrac{{S{A^2}}}{{2SO}} = \dfrac{{{{\left( {a\sqrt 6 } \right)}^2}}}{{2.a\sqrt 3 }} = \dfrac{3}{{\sqrt 3 }}a\end{array}\)
Vcầu \( = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {\left( {\dfrac{3}{{\sqrt 3 }}a} \right)^3} = 4\sqrt 3 .\pi .{a^3}\)
Chọn C







