Lời giải chi tiết:

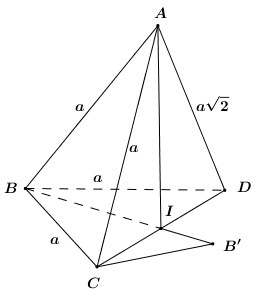
\( + )\) Gọi \(I\) là trung điểm \(CD\). Do \(BC = BD \Rightarrow BI \bot CD.\)

\( + )\) Vì \(\left( {ACD} \right) \bot \left( {BCD} \right)\) nên \(BI \bot \left( {ACD} \right)\).

\( + )\) Xét \(\Delta AIB\) và \(\Delta CIB\) có: \(BI\) chung;

\(\widehat {AIB} = \widehat {CIB} = {90^0},\,\,AB = CB = a\).

\( \Rightarrow \Delta AIB = \Delta DIB\,\,\left( {canh\,\,huyen - canh\,\,goc\,vuong} \right) \Rightarrow AI = CI\)

\( \Rightarrow AI = \dfrac{1}{2}CD \Rightarrow \Delta ACD\) vuông tại \(A\).

\( \Rightarrow \) Tâm mặt cầu ngoại tiếp tứ diện thuộc \(BI\).

\( + )\) Tâm mặt cầu ngoại tiếp \(ABCD\) là tâm đường tròn ngoại tiếp \(\Delta BCD\).

Gọi \(R\) là bán kính đường tròn ngoại tiếp \(\Delta BCD\)\( \Rightarrow BB' = 2R\).

\( + )\) Xét \(\Delta CIB\) và \(\Delta B'CB\) có:

\(\widehat {CIB} = \widehat {B'CB} = {90^0};\,\,\widehat B\,\,chung\).

\( \Rightarrow \) \(\Delta CIB\) đồng dạng \(\Delta B'CB\) (g.g)

\( \Rightarrow  \Rightarrow \dfrac{{CB}}{{BI}} = \dfrac{{BB'}}{{CB}} \Leftrightarrow C{B^2} = BI.BB' = 2R.BI \Rightarrow R = \dfrac{{C{B^2}}}{{2.BI}}\)

\( + )\) Xét \(\Delta BCI\) có:

\(\begin{array}{l}B{I^2} = B{C^2} - \dfrac{{C{D^2}}}{4} = B{C^2} - \dfrac{{A{C^2} + A{D^2}}}{4} = {a^2} - \dfrac{{{a^2} + {{\left( {a\sqrt 2 } \right)}^2}}}{4} \Rightarrow BI = \dfrac{a}{2}\\ \Rightarrow {R_{mcnt}} = \dfrac{{C{B^2}}}{{2.BI}} = \dfrac{{{a^2}}}{{2.\dfrac{a}{2}}} = a \Rightarrow {S_{xq}} = 4\pi {a^2}.\end{array}\)        

Chọn A.