Câu hỏi
Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), \(AB = a\sqrt 2 \), các cạnh bên \(SA = SB = SC\). Góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({60^0}\). Tính bán kính mặt cầu ngoại tiếp khối chóp \(S.ABC\).
- A \(\dfrac{{2a}}{{\sqrt 6 }}.\)
- B \(\dfrac{{2a}}{3}.\)
- C \(\dfrac{{2a}}{{\sqrt 3 }}.\)
- D \(\dfrac{{2a}}{{\sqrt 2 }}.\)
Lời giải chi tiết:
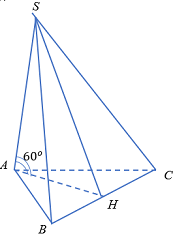
\( + )\) Gọi \(H\) là trung điểm \(BC\).
Vì \(\Delta ABC\) vuông cân \( \Rightarrow HA = HB = HC.\)
Mà \(SA = SB = SC \Rightarrow SH \bot BC\)
\( \Rightarrow \) Góc giữa \(SA\) và \(\left( {ABC} \right)\) là góc \(\widehat {SAH} = {60^0}\).
\( + )\)\(\Delta ABC\) vuông cân \( \Rightarrow AC = AB = a\sqrt 2 \)
\( \Rightarrow BC = 2a \Rightarrow AH = \dfrac{1}{2}BC = \dfrac{1}{2}.2a = a\).
\( + )\)\(\Delta SHA\) vuông: \(SH = AH.\tan {60^0} = a\sqrt 3 \)
\(SA = \dfrac{{SH}}{{\sin {{60}^0}}} = \dfrac{{a\sqrt 3 }}{{\dfrac{{\sqrt 3 }}{2}}} = 2a\)
\( \Rightarrow {R_{mcnt}} = \dfrac{{S{A^2}}}{{2.SH}} = \dfrac{{{{\left( {2a} \right)}^2}}}{{2.a\sqrt 3 }} = \dfrac{{2a}}{{\sqrt 3 }}\)
Chọn C







