Câu hỏi
Cho hình chóp \(S.ABCD\) có \(SA = SB = SC = SD = \sqrt 5 \), \(ABCD\)nội tiếp đường tròn có bán kính \(r = 1\). Mặt cầu ngoại tiếp \(S.ABCD\)có bán kính là:
- A \(\dfrac{1}{2}\).
- B \(\dfrac{5}{4}\)
- C \(\dfrac{1}{4}\)
- D \(\dfrac{3}{4}\).
Lời giải chi tiết:
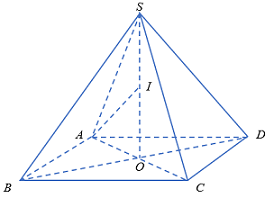
\( + )\)\(ABCD\) nội tiếp đường tròn có \(r = 1 \Rightarrow OA = 1.\)
\( + )\)Xét \(\Delta SOA\) có: \(S{A^2} = S{O^2} + O{A^2}\)
\( \Rightarrow S{O^2} = S{A^2} - O{A^2} = 5 - 1 = 4 \Rightarrow SO = 2\)
\( + )\)\({R_{mcnt}} = \dfrac{{S{A^2}}}{{2.SO}} = \dfrac{{{{\left( {\sqrt 5 } \right)}^2}}}{{2.2}} = \dfrac{5}{4}\)
Chọn B
Câu hỏi trước
