Câu hỏi
Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy bằng \(a\) và cạnh bên bằng \(\dfrac{{a\sqrt {21} }}{6}.\) Gọi \(h,\,\,R\) lần lượt là chiều cao và bán kính mặt cầu ngoại tiếp khối chóp. Tỉ số \(\dfrac{R}{h}\) bằng
- A \(\dfrac{7}{{6}}.\)
- B \(\dfrac{7}{{2}}.\)
- C \(\dfrac{7}{4}.\)
- D \(\dfrac{1}{2}.\)
Lời giải chi tiết:
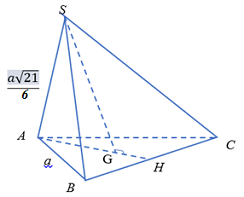
\(R = \dfrac{{S{A^2}}}{{2SG}} = \dfrac{{S{A^2}}}{{2h}} \Rightarrow \dfrac{R}{h} = \dfrac{{S{A^2}}}{{2{h^2}}} = \dfrac{{S{A^2}}}{{2S{G^2}}}\)
+ \(AG = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).
+ Tam giác \(SAG\) có \(\widehat {SGA} = {90^0}\):
\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {\dfrac{{7{a^2}}}{{12}} - \dfrac{{{a^2}}}{3}} = \dfrac{a}{2}\) (Định lí Pytago).
Vậy \(\dfrac{R}{h} = \dfrac{{{{\left( {\dfrac{{a\sqrt {21} }}{6}} \right)}^2}}}{{2.\dfrac{a^2}{4}}} = \dfrac{7}{6}\).
Chọn A.
Câu hỏi trước
