Câu hỏi
Một tứ diện đều có độ dài mỗi cạnh là 2. Tính thể tích khối cầu ngoại tiếp tứ diện này.
- A \(\sqrt 6 \pi \)
- B \(2\sqrt 6 \pi \)
- C \(\dfrac{{\sqrt 6 }}{3}\pi \)
- D \(6\pi \)
Lời giải chi tiết:
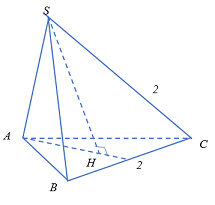
\( + )\)\({V_{SABC}} = \dfrac{{\sqrt 2 }}{{12}}{.2^3} = \dfrac{{2\sqrt 2 }}{3}\)
\( + )\) Gọi \(H\) là trọng tâm \(\Delta ABC\)\( \Rightarrow SH \bot \left( {ABC} \right)\)
\( + )\)Có \({V_{SABC}} = \dfrac{1}{3}.SH.{S_{\Delta ABC}} \Leftrightarrow \dfrac{{2\sqrt 2 }}{3} = \dfrac{1}{3}.SH.\dfrac{{\sqrt 3 }}{4}{.2^2} \Rightarrow SH = \dfrac{{2\sqrt 6 }}{3}\)
\( \Rightarrow R = \dfrac{{S{C^2}}}{{2.SH}} = \dfrac{{{2^2}}}{{2.\dfrac{{2\sqrt 6 }}{3}}} = \dfrac{{\sqrt 6 }}{2}\)
\( \Rightarrow \)Vcầu \( = \dfrac{4}{3}\pi .{R^3} = \dfrac{4}{3}\pi .{\left( {\dfrac{{\sqrt 6 }}{2}} \right)^3} = \pi \sqrt 6 \).
Chọn A
Câu hỏi trước
