Câu hỏi
Cho lăng trụ đứng \(ABC.A'B'C',\) cạnh \(AB = AC = a,\,\,BC = a\sqrt 3 \), \(AA' = 2a.\) Bán kínhmặt cầu ngoại tiếp tứ diện \(AB'C'C\) bằng:
- A \(R = a.\)
- B \(R = a\sqrt 5 .\)
- C \(R = a\sqrt 3 .\)
- D \(R = a\sqrt 2 .\)
Lời giải chi tiết:
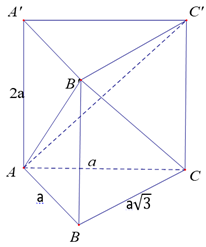
+ Dễ thấy tâm mặt cầu ngoại tiếp tứ diện \(AB'C'C\) cũng là tâm mặt cầu ngoại tiếp lăng trụ \(ABC.A'B'C'.\)
\( \Rightarrow R = \sqrt {{{\left( {\dfrac{{A'A}}{2}} \right)}^2} + {r^2}_{day}} \)
+ Ta có:
\(\cos \widehat {BAC} = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \dfrac{{{a^2} + {a^2} - 3{a^2}}}{{2{a^2}}} = \dfrac{{ - 1}}{2} \Rightarrow \widehat {BAC} = {120^0}\)
+ \({r_{day}} = \dfrac{{BC}}{{2.\sin \widehat {BAC}}} = \dfrac{{a\sqrt 3 }}{{2\sin {{120}^0}}} = a\)
\( \Rightarrow R = \sqrt {{{\left( {\dfrac{{2a}}{2}} \right)}^2} + {a^2}} = a\sqrt 2 .\)
Chọn D
Câu hỏi trước
