Lời giải chi tiết:

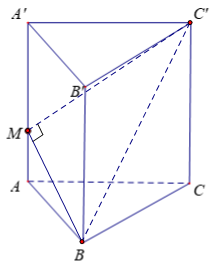
Áp dụng định lí Pytago trong các tam giác vuông ta có:

\(\begin{array}{l}MC' = A'C{'^2} + A'{M^2} = {a^2} + {\left( {\dfrac{2}{3}h} \right)^2}\\M{B^2} = A{M^2} + A{B^2} = {\left( {\dfrac{1}{3}h} \right)^2} + {a^2}\\BC' = C'{C^2} + B{C^2} = {h^2} + {a^2}\end{array}\)

+ \(\Delta MBC'\)vuông tại \(M \Rightarrow M{B^2} + MC{'^2} = BC{'^2}\).

\(\begin{array}{l} \Rightarrow {a^2} + \dfrac{4}{9}{h^2} + \dfrac{1}{9}{h^2} + {a^2} = {h^2} + {a^2}\\ \Leftrightarrow \dfrac{5}{9}{h^2} + 2{a^2} = {h^2} + {a^2} \Leftrightarrow \dfrac{{4{h^2}}}{9} = {a^2} \Leftrightarrow h = \dfrac{{3a}}{2}\end{array}\)

+ \(\Delta ABC\) là tam giác đều \( \Rightarrow {R_d} = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)

\(\begin{array}{l}{R_{mcnt}} = \sqrt {{R_d}^2 + \dfrac{{{h^2}}}{4}}  = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2} + \dfrac{{{{\left( {\dfrac{{3a}}{2}} \right)}^2}}}{4}}  = a\dfrac{{\sqrt {129} }}{{12}}\\ \Rightarrow V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi .\dfrac{{129\sqrt {129} }}{{1728}}{a^3} = \dfrac{{43\pi \sqrt {129} }}{{432}}{a^3}\end{array}\)

Vậy \(\dfrac{V}{{{a^3}}} = \dfrac{{43\pi \sqrt {129} }}{{432}} \approx 3,5516\).

Chọn B