Câu hỏi
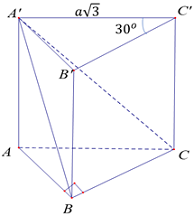
Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(B,\)\(AC = a\sqrt 3 ;\)\(\widehat {ACB} = {30^0}.\) Góc giữa đường thẳng \(A'B\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({60^0}.\) Tính bán kính mặt cầu ngoại tiếp tứ diện \(A'.ABC.\)
- A \(\dfrac{{3a}}{4}.\)
- B \(\dfrac{{a\sqrt {21} }}{4}.\)
- C \(\dfrac{{a\sqrt {21} }}{2}.\)
- D \(\dfrac{{a\sqrt {21} }}{8}.\)
Lời giải chi tiết:
+ \(\sin \widehat {ACB} = \sin {30^0} \Leftrightarrow \dfrac{{AB}}{{AC}} = \dfrac{1}{2} \Leftrightarrow AB = \dfrac{{a\sqrt 3 }}{2}\).
+ Góc giữa \(A'B\)và \(\left( {ABC} \right)\).
\(A'A \bot \left( {ABC} \right)\),
Điểm chung: \(B\).
\( \Rightarrow \widehat {\left( {A'B;\left( {ABC} \right)} \right)} = \widehat {\left( {A'B;AB} \right)} = \widehat {A'BA} = {60^0}\)
+ Xét \(\Delta A'BA\) vuông tại \(A\) có:
\(\tan \widehat {A'BA} = {60^0} \Leftrightarrow \dfrac{{AA'}}{{AB}} = \sqrt 3 \Leftrightarrow AA' = \dfrac{{3a}}{2}\).
+ Xét đáy \(ABC\) là tam giác vuông\( \Rightarrow \)Tâm đường tròn ngoại tiếp đáy là trung điểm \(AC \Rightarrow {r_{day}} = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 3 }}{2}\).
+ Tứ diện \(A'.ABC\) có:\(h = AA' = \dfrac{{3a}}{2};\,\,{r_{day}} = \dfrac{{a\sqrt 3 }}{2}\).
\( \Rightarrow \) Bán kính mặt cầu ngoại tiếp tứ diện là:\(R = \sqrt {{{\left( {\dfrac{h}{2}} \right)}^2} + {r^2}_{day}} = \sqrt {{{\left( {\dfrac{{3a}}{4}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2}} = \dfrac{{a\sqrt {21} }}{4}\).
Chọn B







