Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = 2a,\,\,AD = a.\) Cạnh bên \(SA\)vuông góc với đáy và góc giữa \(SC\)với đáy bằng \({45^0}.\) Gọi \(N\) là trung điểm của \(SA,\)\(h\) là chiều cao của khối chóp \(S.ABCD\) và \(R\) là bán kính mặt cầu ngoại tiếp \(N.ABC.\) Mệnh đề nào dưới đây đúng ?
- A \(4R = \sqrt {5\,} h.\)
- B \(\sqrt 5 \,R = 4h.\)
- C \(R = \dfrac{4}{{5\sqrt 5 }}h.\)
- D \(R = \dfrac{{5\sqrt 5 }}{4}h.\)
Lời giải chi tiết:
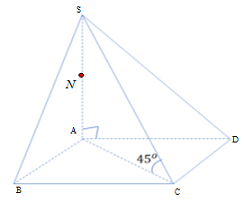
+ \(\widehat {\left( {SC;\left( {ABCD} \right)} \right)} = {45^0}\)
Có: \(C\) chung; \(SA \bot \left( {ABCD} \right)\)
\( \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {SCA} = {45^0}\)
+ Xét \(\Delta SAC\,\,\,\left( {\widehat {SAC} = {{90}^0}} \right)\): \(\tan {45^0} = \dfrac{{SA}}{{AC}} = \dfrac{h}{{AC}} \Rightarrow AC = h\).
+ Có: \({R_{NABC}} = \sqrt {\dfrac{{N{A^2}}}{4} + {r^2}_{\Delta ABC}} \,\,\,\,\,\left( * \right)\)
+ Xét \(\Delta ABC\,\,\,\left( {\widehat {ABC} = {{90}^0}} \right) \Rightarrow {r_{\Delta ABC}} = \dfrac{{AC}}{2} = \dfrac{h}{2}\)
\(\begin{array}{l} \Rightarrow ( * ) \Leftrightarrow R = \sqrt {\dfrac{{{{\left( {\dfrac{h}{2}} \right)}^2}}}{4} + {{\left( {\dfrac{h}{2}} \right)}^2}} \Leftrightarrow R = \sqrt {\dfrac{{{h^2}}}{{16}} + \dfrac{{{h^2}}}{4}} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,R = \sqrt {\dfrac{5}{{16}}{h^2}} \Leftrightarrow \,R = \dfrac{{\sqrt 5 }}{4}h \Leftrightarrow 4R = \sqrt 5 h\end{array}\)
Chọn A







