Lời giải chi tiết:

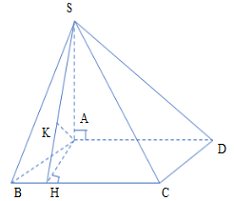
Ta có: \(d\left( {AD;SC} \right) = d\left( {AD;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right) = \dfrac{{3a}}{2}.\)

+ Xét hình thoi \(ABCD\): Từ \(A\) kẻ \(AH \bot BC\).

+ Xét \(\Delta SAH:\) Kẻ \(AK \bot SH\,\,\,\left( {K \in SH} \right)\)  ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AH\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAH} \right) \Rightarrow BC \bot AK\\\left\{ \begin{array}{l}AK \bot BC\\AK \bot SH\end{array} \right. \Rightarrow AK \bot \left( {SBC} \right) \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AK = \dfrac{{3a}}{2}\end{array}\)

+ Xét \(ABCD\) có \(\widehat {BAD} = {120^0} \Rightarrow \widehat {BAC} = \widehat {CAD} = \dfrac{{{{120}^0}}}{2} = {60^0}\)

+ Mà \(AB = BC\) (\(ABCD\) là hình thoi) \( \Rightarrow \Delta ABC\)đều cạnh \(2a\).

\( \Rightarrow AH = \dfrac{{\sqrt 3 }}{2}.2a = \sqrt 3 a\)

+ Xét \(\Delta SAH\,\,\) (\(\widehat {SAH} = {90^0},\,\,AK\) là đường cao) ta có: \(\dfrac{1}{{A{K^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{H^2}}}\) (Hệ thức lượng).

\( \Rightarrow \dfrac{4}{{9{a^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{3{a^2}}} \Leftrightarrow S{A^2} = 9{a^2} \Leftrightarrow SA = 3a.\)

+ Xét hình thoi \(ABCD\) có: \(AB = BC = CD = AD = AC\).

\( \Rightarrow CA\) là bán kính đường tròn ngoại tiếp \(\Delta BAD\)\( \Rightarrow {r_{\Delta BAD}} = CA = 2a\).

\( \Rightarrow {R_{SABD}} = \sqrt {\dfrac{{S{A^2}}}{4} + {{\left( {{r_{\Delta BAD}}} \right)}^2}}  = \sqrt {\dfrac{{{{\left( {3a} \right)}^2}}}{4} + {{\left( {2a} \right)}^2}}  = \dfrac{{5a}}{2}.\)

Chọn B